Max Schröder
Lifted Filtering via Exchangeable Decomposition
May 07, 2018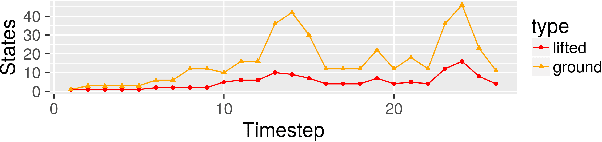
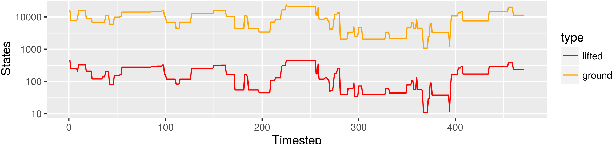
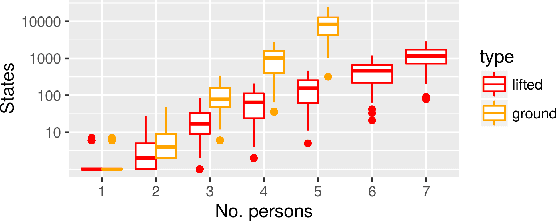
Abstract:We present a model for exact recursive Bayesian filtering based on lifted multiset states. Combining multisets with lifting makes it possible to simultaneously exploit multiple strategies for reducing inference complexity when compared to list-based grounded state representations. The core idea is to borrow the concept of Maximally Parallel Multiset Rewriting Systems and to enhance it by concepts from Rao-Blackwellization and Lifted Inference, giving a representation of state distributions that enables efficient inference. In worlds where the random variables that define the system state are exchangeable -- where the identity of entities does not matter -- it automatically uses a representation that abstracts from ordering (achieving an exponential reduction in complexity) -- and it automatically adapts when observations or system dynamics destroy exchangeability by breaking symmetry.
State-Space Abstractions for Probabilistic Inference: A Systematic Review
Apr 23, 2018

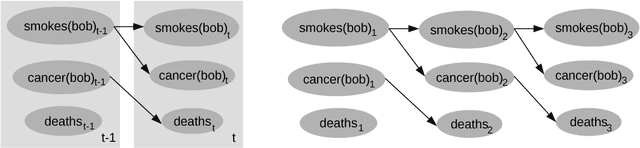

Abstract:Tasks such as social network analysis, human behavior recognition, or modeling biochemical reactions, can be solved elegantly by using the probabilistic inference framework. However, standard probabilistic inference algorithms work at a propositional level, and thus cannot capture the symmetries and redundancies that are present in these tasks. Algorithms that exploit those symmetries have been devised in different research fields, for example by the lifted inference-, multiple object tracking-, and modeling and simulation-communities. The common idea, that we call state space abstraction, is to perform inference over compact representations of sets of symmetric states. Although they are concerned with a similar topic, the relationship between these approaches has not been investigated systematically. This survey provides the following contributions. We perform a systematic literature review to outline the state of the art in probabilistic inference methods exploiting symmetries. From an initial set of more than 4,000 papers, we identify 116 relevant papers. Furthermore, we provide new high-level categories that classify the approaches, based on the problem classes the different approaches can solve. Researchers from different fields that are confronted with a state space explosion problem in a probabilistic system can use this classification to identify possible solutions. Finally, based on this conceptualization, we identify potentials for future research, as some relevant application domains are not addressed by current approaches.
Sequential Lifted Bayesian Filtering in Multiset Rewriting Systems
Aug 14, 2017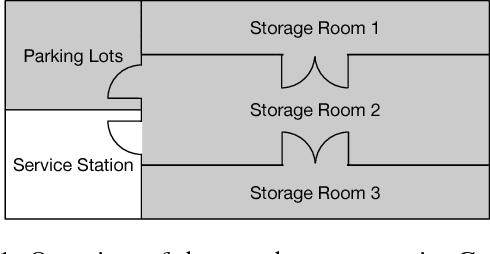
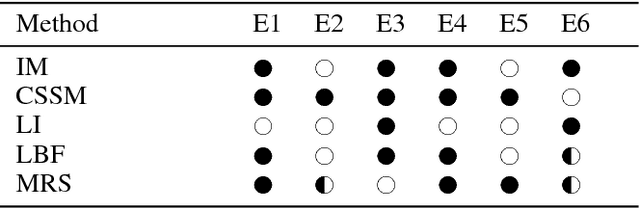
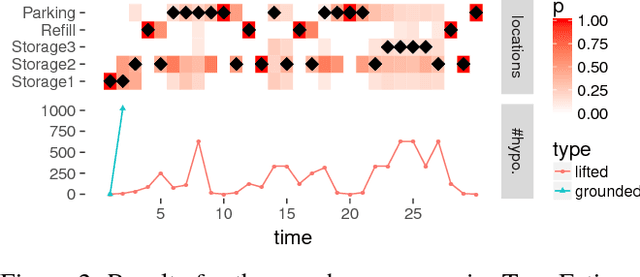
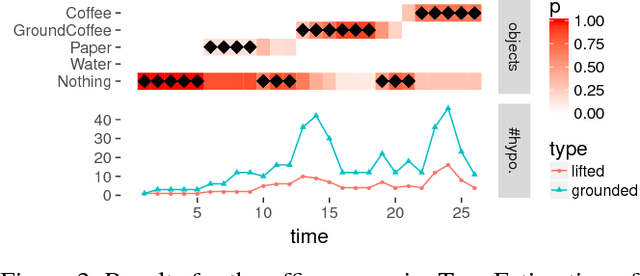
Abstract:Bayesian Filtering for plan and activity recognition is challenging for scenarios that contain many observation equivalent entities (i.e. entities that produce the same observations). This is due to the combinatorial explosion in the number of hypotheses that need to be tracked. However, this class of problems exhibits a certain symmetry that can be exploited for state space representation and inference. We analyze current state of the art methods and find that none of them completely fits the requirements arising in this problem class. We sketch a novel inference algorithm that provides a solution by incorporating concepts from Lifted Inference algorithms, Probabilistic Multiset Rewriting Systems, and Computational State Space Models. Two experiments confirm that this novel algorithm has the potential to perform efficient probabilistic inference on this problem class.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge