Lifted Filtering via Exchangeable Decomposition
Paper and Code
May 07, 2018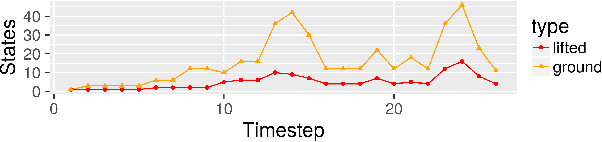
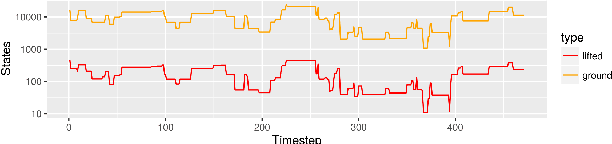
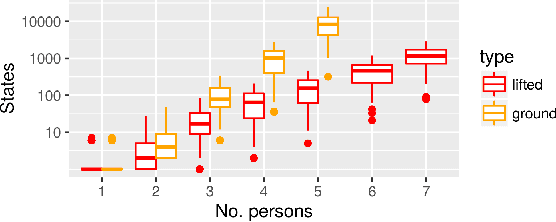
We present a model for exact recursive Bayesian filtering based on lifted multiset states. Combining multisets with lifting makes it possible to simultaneously exploit multiple strategies for reducing inference complexity when compared to list-based grounded state representations. The core idea is to borrow the concept of Maximally Parallel Multiset Rewriting Systems and to enhance it by concepts from Rao-Blackwellization and Lifted Inference, giving a representation of state distributions that enables efficient inference. In worlds where the random variables that define the system state are exchangeable -- where the identity of entities does not matter -- it automatically uses a representation that abstracts from ordering (achieving an exponential reduction in complexity) -- and it automatically adapts when observations or system dynamics destroy exchangeability by breaking symmetry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge