$ρ$-VAE: Autoregressive parametrization of the VAE encoder

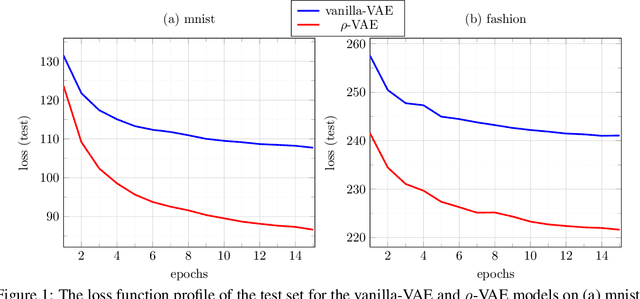
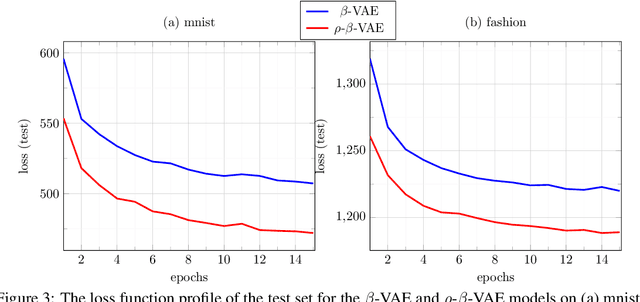
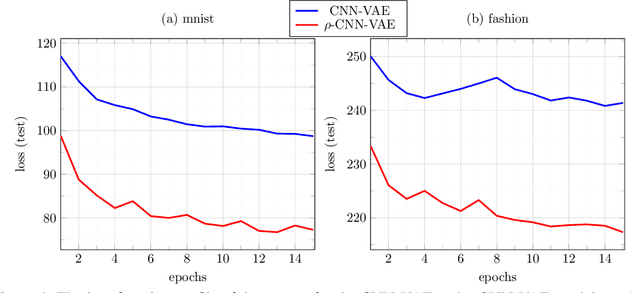
We make a minimal, but very effective alteration to the VAE model. This is about a drop-in replacement for the (sample-dependent) approximate posterior to change it from the standard white Gaussian with diagonal covariance to the first-order autoregressive Gaussian. We argue that this is a more reasonable choice to adopt for natural signals like images, as it does not force the existing correlation in the data to disappear in the posterior. Moreover, it allows more freedom for the approximate posterior to match the true posterior. This allows for the repararametrization trick, as well as the KL-divergence term to still have closed-form expressions, obviating the need for its sample-based estimation. Although providing more freedom to adapt to correlated distributions, our parametrization has even less number of parameters than the diagonal covariance, as it requires only two scalars, $\rho$ and $s$, to characterize correlation and scaling, respectively. As validated by the experiments, our proposition noticeably and consistently improves the quality of image generation in a plug-and-play manner, needing no further parameter tuning, and across all setups. The code to reproduce our experiments is available at \url{https://github.com/sssohrab/rho_VAE/}.

Variational Saccading: Efficient Inference for Large Resolution Images

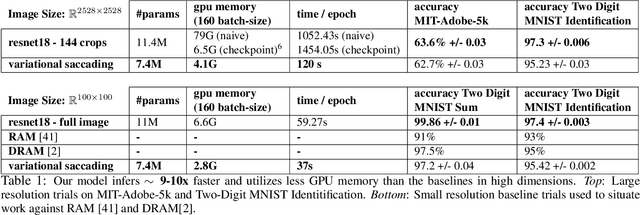
Image classification with deep neural networks is typically restricted to images of small dimensionality such as 224x244 in Resnet models. This limitation excludes the 4000x3000 dimensional images that are taken by modern smartphone cameras and smart devices. In this work, we aim to mitigate the prohibitive inferential and memory costs of operating in such large dimensional spaces. To sample from the high-resolution original input distribution, we propose using a smaller proxy distribution to learn the co-ordinates that correspond to regions of interest in the high-dimensional space. We introduce a new principled variational lower bound that captures the relationship of the proxy distribution's posterior and the original image's co-ordinate space in a way that maximizes the conditional classification likelihood. We empirically demonstrate on one synthetic benchmark and one real world large resolution DSLR camera image dataset that our method produces comparable results with 10x faster inference and lower memory consumption than a model that utilizes the entire original input distribution.