On associative neural networks for sparse patterns with huge capacities

Generalized Hopfield models with higher-order or exponential interaction terms are known to have substantially larger storage capacities than the classical quadratic model. On the other hand, associative memories for sparse patterns, such as the Willshaw and Amari models, already outperform the classical Hopfield model in the sparse regime. In this paper we combine these two mechanisms. We introduce higher-order versions of sparse associative memory models and study their storage capacities. For fixed interaction order $n$, we obtain storage capacities of polynomial order in the system size. When the interaction order is allowed to grow logarithmically with the number of neurons, this yields super-polynomial capacities. We also discuss an analogue in the Gripon--Berrou architecture which was formulated for non-sparse messages (see \cite{griponc}). Our results show that the capacity increase caused by higher-order interactions persists in the sparse setting, although the precise storage scale depends on the underlying architecture.

Some Remarks on Replicated Simulated Annealing

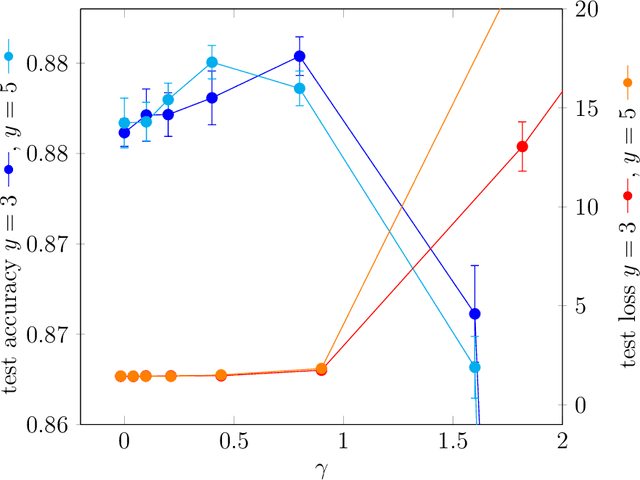
Recently authors have introduced the idea of training discrete weights neural networks using a mix between classical simulated annealing and a replica ansatz known from the statistical physics literature. Among other points, they claim their method is able to find robust configurations. In this paper, we analyze this so-called "replicated simulated annealing" algorithm. In particular, we explicit criteria to guarantee its convergence, and study when it successfully samples from configurations. We also perform experiments using synthetic and real data bases.

Towards an Intrinsic Definition of Robustness for a Classifier

The robustness of classifiers has become a question of paramount importance in the past few years. Indeed, it has been shown that state-of-the-art deep learning architectures can easily be fooled with imperceptible changes to their inputs. Therefore, finding good measures of robustness of a trained classifier is a key issue in the field. In this paper, we point out that averaging the radius of robustness of samples in a validation set is a statistically weak measure. We propose instead to weight the importance of samples depending on their difficulty. We motivate the proposed score by a theoretical case study using logistic regression, where we show that the proposed score is independent of the choice of the samples it is evaluated upon. We also empirically demonstrate the ability of the proposed score to measure robustness of classifiers with little dependence on the choice of samples in more complex settings, including deep convolutional neural networks and real datasets.

Improving Accuracy of Nonparametric Transfer Learning via Vector Segmentation

Transfer learning using deep neural networks as feature extractors has become increasingly popular over the past few years. It allows to obtain state-of-the-art accuracy on datasets too small to train a deep neural network on its own, and it provides cutting edge descriptors that, combined with nonparametric learning methods, allow rapid and flexible deployment of performing solutions in computationally restricted settings. In this paper, we are interested in showing that the features extracted using deep neural networks have specific properties which can be used to improve accuracy of downstream nonparametric learning methods. Namely, we demonstrate that for some distributions where information is embedded in a few coordinates, segmenting feature vectors can lead to better accuracy. We show how this model can be applied to real datasets by performing experiments using three mainstream deep neural network feature extractors and four databases, in vision and audio.

Associative Memories to Accelerate Approximate Nearest Neighbor Search

Nearest neighbor search is a very active field in machine learning for it appears in many application cases, including classification and object retrieval. In its canonical version, the complexity of the search is linear with both the dimension and the cardinal of the collection of vectors the search is performed in. Recently many works have focused on reducing the dimension of vectors using quantization techniques or hashing, while providing an approximate result. In this paper we focus instead on tackling the cardinal of the collection of vectors. Namely, we introduce a technique that partitions the collection of vectors and stores each part in its own associative memory. When a query vector is given to the system, associative memories are polled to identify which one contain the closest match. Then an exhaustive search is conducted only on the part of vectors stored in the selected associative memory. We study the effectiveness of the system when messages to store are generated from i.i.d. uniform $\pm$1 random variables or 0-1 sparse i.i.d. random variables. We also conduct experiment on both synthetic data and real data and show it is possible to achieve interesting trade-offs between complexity and accuracy.