Matthew Sotoudeh
Provable Repair of Deep Neural Networks
Apr 25, 2021



Abstract:Deep Neural Networks (DNNs) have grown in popularity over the past decade and are now being used in safety-critical domains such as aircraft collision avoidance. This has motivated a large number of techniques for finding unsafe behavior in DNNs. In contrast, this paper tackles the problem of correcting a DNN once unsafe behavior is found. We introduce the provable repair problem, which is the problem of repairing a network N to construct a new network N' that satisfies a given specification. If the safety specification is over a finite set of points, our Provable Point Repair algorithm can find a provably minimal repair satisfying the specification, regardless of the activation functions used. For safety specifications addressing convex polytopes containing infinitely many points, our Provable Polytope Repair algorithm can find a provably minimal repair satisfying the specification for DNNs using piecewise-linear activation functions. The key insight behind both of these algorithms is the introduction of a Decoupled DNN architecture, which allows us to reduce provable repair to a linear programming problem. Our experimental results demonstrate the efficiency and effectiveness of our Provable Repair algorithms on a variety of challenging tasks.
SyReNN: A Tool for Analyzing Deep Neural Networks
Jan 09, 2021



Abstract:Deep Neural Networks (DNNs) are rapidly gaining popularity in a variety of important domains. Formally, DNNs are complicated vector-valued functions which come in a variety of sizes and applications. Unfortunately, modern DNNs have been shown to be vulnerable to a variety of attacks and buggy behavior. This has motivated recent work in formally analyzing the properties of such DNNs. This paper introduces SyReNN, a tool for understanding and analyzing a DNN by computing its symbolic representation. The key insight is to decompose the DNN into linear functions. Our tool is designed for analyses using low-dimensional subsets of the input space, a unique design point in the space of DNN analysis tools. We describe the tool and the underlying theory, then evaluate its use and performance on three case studies: computing Integrated Gradients, visualizing a DNN's decision boundaries, and patching a DNN.
Analogy-Making as a Core Primitive in the Software Engineering Toolbox
Sep 14, 2020



Abstract:An analogy is an identification of structural similarities and correspondences between two objects. Computational models of analogy making have been studied extensively in the field of cognitive science to better understand high-level human cognition. For instance, Melanie Mitchell and Douglas Hofstadter sought to better understand high-level perception by developing the Copycat algorithm for completing analogies between letter sequences. In this paper, we argue that analogy making should be seen as a core primitive in software engineering. We motivate this argument by showing how complex software engineering problems such as program understanding and source-code transformation learning can be reduced to an instance of the analogy-making problem. We demonstrate this idea using Sifter, a new analogy-making algorithm suitable for software engineering applications that adapts and extends ideas from Copycat. In particular, Sifter reduces analogy-making to searching for a sequence of update rule applications. Sifter uses a novel representation for mathematical structures capable of effectively representing the wide variety of information embedded in software. We conclude by listing major areas of future work for Sifter and analogy-making in software engineering.
Abstract Neural Networks
Sep 11, 2020


Abstract:Deep Neural Networks (DNNs) are rapidly being applied to safety-critical domains such as drone and airplane control, motivating techniques for verifying the safety of their behavior. Unfortunately, DNN verification is NP-hard, with current algorithms slowing exponentially with the number of nodes in the DNN. This paper introduces the notion of Abstract Neural Networks (ANNs), which can be used to soundly overapproximate DNNs while using fewer nodes. An ANN is like a DNN except weight matrices are replaced by values in a given abstract domain. We present a framework parameterized by the abstract domain and activation functions used in the DNN that can be used to construct a corresponding ANN. We present necessary and sufficient conditions on the DNN activation functions for the constructed ANN to soundly over-approximate the given DNN. Prior work on DNN abstraction was restricted to the interval domain and ReLU activation function. Our framework can be instantiated with other abstract domains such as octagons and polyhedra, as well as other activation functions such as Leaky ReLU, Sigmoid, and Hyperbolic Tangent.
A Symbolic Neural Network Representation and its Application to Understanding, Verifying, and Patching Networks
Aug 20, 2019



Abstract:Analysis and manipulation of trained neural networks is a challenging and important problem. We propose a symbolic representation for piecewise-linear neural networks and discuss its efficient computation. With this representation, one can translate the problem of analyzing a complex neural network into that of analyzing a finite set of affine functions. We demonstrate the use of this representation for three applications. First, we apply the symbolic representation to computing weakest preconditions on network inputs, which we use to exactly visualize the advisories made by a network meant to operate an aircraft collision avoidance system. Second, we use the symbolic representation to compute strongest postconditions on the network outputs, which we use to perform bounded model checking on standard neural network controllers. Finally, we show how the symbolic representation can be combined with a new form of neural network to perform patching; i.e., correct user-specified behavior of the network.
Computing Linear Restrictions of Neural Networks
Aug 17, 2019



Abstract:A linear restriction of a function is the same function with its domain restricted to points on a given line. This paper addresses the problem of computing a succinct representation for a linear restriction of a piecewise-linear neural network. This primitive, which we call ExactLine, allows us to exactly characterize the result of applying the network to all of the infinitely many points on a line. In particular, ExactLine computes a partitioning of the given input line segment such that the network is affine on each partition. We present an efficient algorithm for computing ExactLine for networks that use ReLU, MaxPool, batch normalization, fully-connected, convolutional, and other layers, along with several applications. First, we show how to exactly determine decision boundaries of an ACAS Xu neural network, providing significantly improved confidence in the results compared to prior work that sampled finitely many points in the input space. Next, we demonstrate how to exactly compute integrated gradients, which are commonly used for neural network attributions, allowing us to show that the prior heuristic-based methods had relative errors of 25-45% and show that a better sampling method can achieve higher accuracy with less computation. Finally, we use ExactLine to empirically falsify the core assumption behind a well-known hypothesis about adversarial examples, and in the process identify interesting properties of adversarially-trained networks.
ISA Mapper: A Compute and Hardware Agnostic Deep Learning Compiler
Oct 12, 2018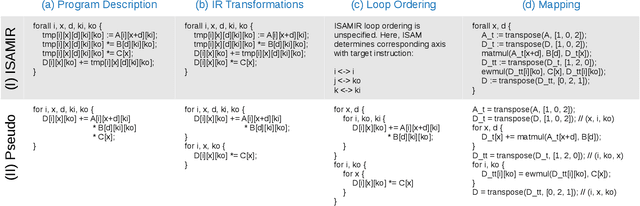
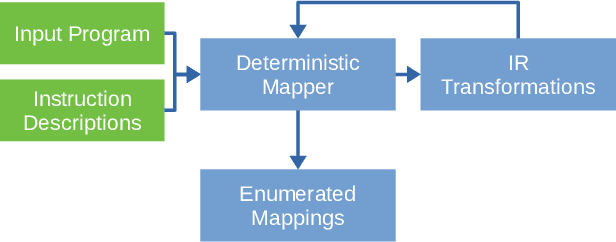
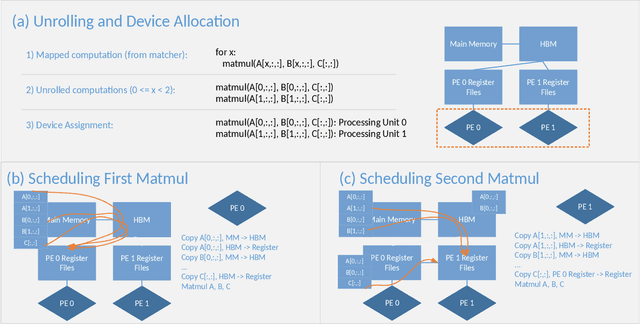
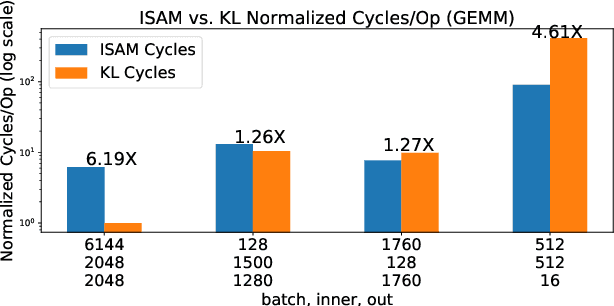
Abstract:Domain specific accelerators present new challenges and opportunities for code generation onto novel instruction sets, communication fabrics, and memory architectures. In this paper we introduce an intermediate representation (IR) which enables both deep learning computational kernels and hardware capabilities to be described in the same IR. We then formulate and apply instruction mapping to determine the possible ways a computation can be performed on a hardware system. Next, our scheduler chooses a specific mapping and determines the data movement and computation order. In order to manage the large search space of mappings and schedules, we developed a flexible framework that allows heuristics, cost models, and potentially machine learning to facilitate this search problem. With this system, we demonstrate the automated extraction of matrix multiplication kernels out of recent deep learning kernels such as depthwise-separable convolution. In addition, we demonstrate two to five times better performance on DeepBench sized GEMMs and GRU RNN execution when compared to state-of-the-art (SOTA) implementations on new hardware and up to 85% of the performance for SOTA implementations on existing hardware.
DeepThin: A Self-Compressing Library for Deep Neural Networks
Feb 20, 2018



Abstract:As the industry deploys increasingly large and complex neural networks to mobile devices, more pressure is put on the memory and compute resources of those devices. Deep compression, or compression of deep neural network weight matrices, is a technique to stretch resources for such scenarios. Existing compression methods cannot effectively compress models smaller than 1-2% of their original size. We develop a new compression technique, DeepThin, building on existing research in the area of low rank factorization. We identify and break artificial constraints imposed by low rank approximations by combining rank factorization with a reshaping process that adds nonlinearity to the approximation function. We deploy DeepThin as a plug-gable library integrated with TensorFlow that enables users to seamlessly compress models at different granularities. We evaluate DeepThin on two state-of-the-art acoustic models, TFKaldi and DeepSpeech, comparing it to previous compression work (Pruning, HashNet, and Rank Factorization), empirical limit study approaches, and hand-tuned models. For TFKaldi, our DeepThin networks show better word error rates (WER) than competing methods at practically all tested compression rates, achieving an average of 60% relative improvement over rank factorization, 57% over pruning, 23% over hand-tuned same-size networks, and 6% over the computationally expensive HashedNets. For DeepSpeech, DeepThin-compressed networks achieve better test loss than all other compression methods, reaching a 28% better result than rank factorization, 27% better than pruning, 20% better than hand-tuned same-size networks, and 12% better than HashedNets. DeepThin also provide inference performance benefits ranging from 2X to 14X speedups, depending on the compression ratio and platform cache sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge