Large Data and Zero Noise Limits of Graph-Based Semi-Supervised Learning Algorithms

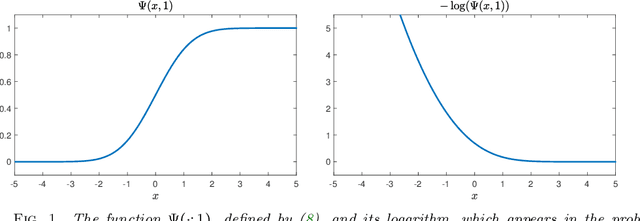
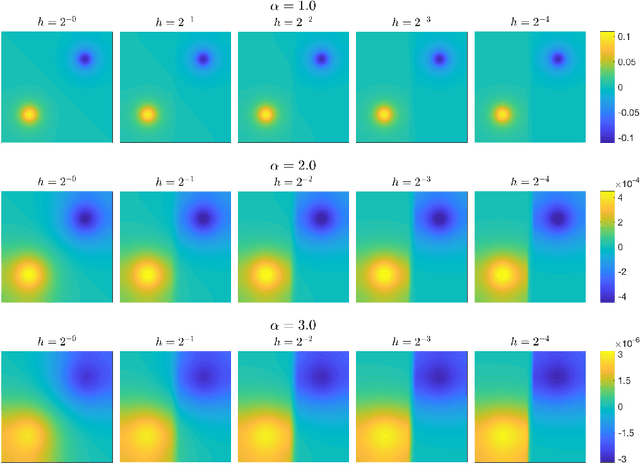
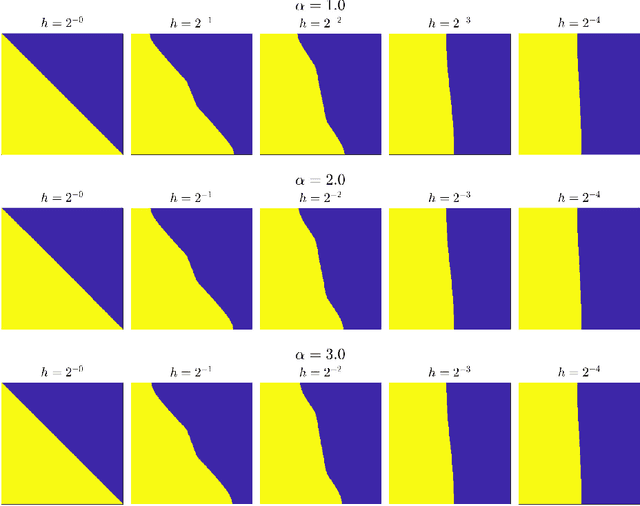
Scalings in which the graph Laplacian approaches a differential operator in the large graph limit are used to develop understanding of a number of algorithms for semi-supervised learning; in particular the extension, to this graph setting, of the probit algorithm, level set and kriging methods, are studied. Both optimization and Bayesian approaches are considered, based around a regularizing quadratic form found from an affine transformation of the Laplacian, raised to a, possibly fractional, exponent. Conditions on the parameters defining this quadratic form are identified under which well-defined limiting continuum analogues of the optimization and Bayesian semi-supervised learning problems may be found, thereby shedding light on the design of algorithms in the large graph setting. The large graph limits of the optimization formulations are tackled through $\Gamma$-convergence, using the recently introduced $TL^p$ metric. The small labelling noise limit of the Bayesian formulations are also identified, and contrasted with pre-existing harmonic function approaches to the problem.

Robust MCMC Sampling with Non-Gaussian and Hierarchical Priors in High Dimensions

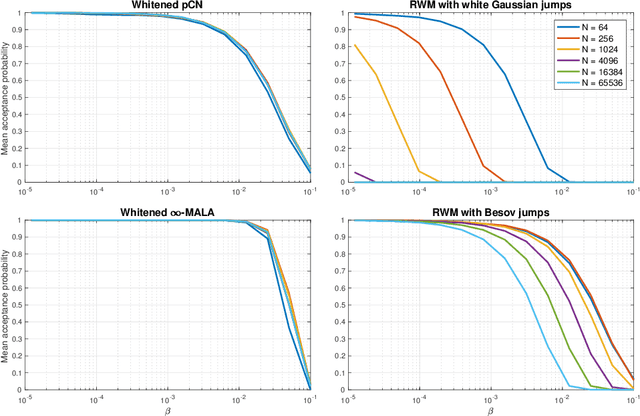
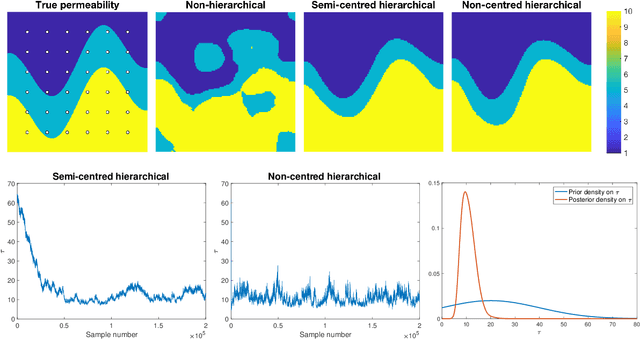
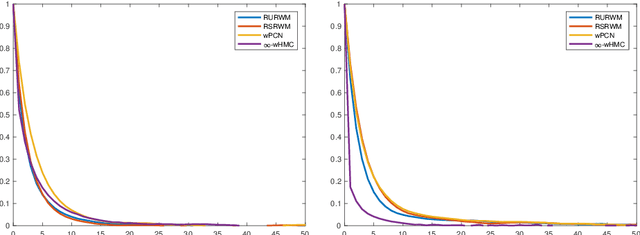
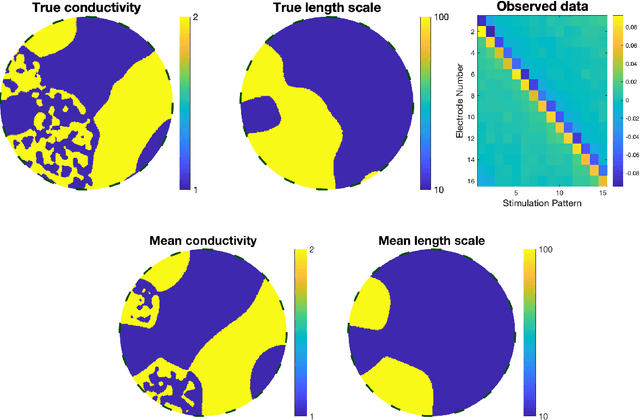
A key problem in inference for high dimensional unknowns is the design of sampling algorithms whose performance scales favourably with the dimension of the unknown. A typical setting in which these problems arise is the area of Bayesian inverse problems. In such problems, which include graph-based learning, nonparametric regression and PDE-based inversion, the unknown can be viewed as an infinite-dimensional parameter (such as a function) that has been discretised. This results in a high-dimensional space for inference. Here we study robustness of an MCMC algorithm for posterior inference; this refers to MCMC convergence rates that do not deteriorate as the discretisation becomes finer. When a Gaussian prior is employed there is a known methodology for the design of robust MCMC samplers. However, one often requires more flexibility than a Gaussian prior can provide: hierarchical models are used to enable inference of parameters underlying a Gaussian prior; or non-Gaussian priors, such as Besov, are employed to induce sparse MAP estimators; or deep Gaussian priors are used to represent other non-Gaussian phenomena; and piecewise constant functions, which are necessarily non-Gaussian, are required for classification problems. The purpose of this article is to show that the simulation technology available for Gaussian priors can be exported to such non-Gaussian priors. The underlying methodology is based on a white noise representation of the unknown. This is exploited both for robust posterior sampling and for joint inference of the function and parameters involved in the specification of its prior, in which case our framework borrows strength from the well-developed non-centred methodology for Bayesian hierarchical models. The desired robustness of the proposed sampling algorithms is supported by some theory and by extensive numerical evidence from several challenging problems.