POMONAG: Pareto-Optimal Many-Objective Neural Architecture Generator

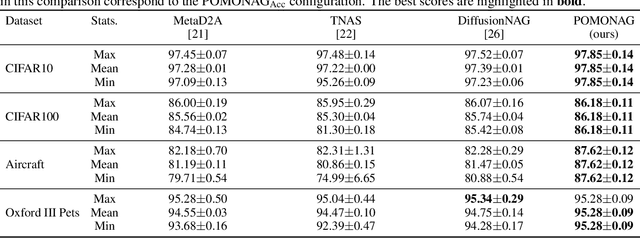
Neural Architecture Search (NAS) automates neural network design, reducing dependence on human expertise. While NAS methods are computationally intensive and dataset-specific, auxiliary predictors reduce the models needing training, decreasing search time. This strategy is used to generate architectures satisfying multiple computational constraints. Recently, Transferable NAS has emerged, generalizing the search process from dataset-dependent to task-dependent. In this field, DiffusionNAG is a state-of-the-art method. This diffusion-based approach streamlines computation, generating architectures optimized for accuracy on unseen datasets without further adaptation. However, by focusing solely on accuracy, DiffusionNAG overlooks other crucial objectives like model complexity, computational efficiency, and inference latency -- factors essential for deploying models in resource-constrained environments. This paper introduces the Pareto-Optimal Many-Objective Neural Architecture Generator (POMONAG), extending DiffusionNAG via a many-objective diffusion process. POMONAG simultaneously considers accuracy, number of parameters, multiply-accumulate operations (MACs), and inference latency. It integrates Performance Predictor models to estimate these metrics and guide diffusion gradients. POMONAG's optimization is enhanced by expanding its training Meta-Dataset, applying Pareto Front Filtering, and refining embeddings for conditional generation. These enhancements enable POMONAG to generate Pareto-optimal architectures that outperform the previous state-of-the-art in performance and efficiency. Results were validated on two search spaces -- NASBench201 and MobileNetV3 -- and evaluated across 15 image classification datasets.

Byzantine-Resilient Learning Beyond Gradients: Distributing Evolutionary Search

Modern machine learning (ML) models are capable of impressive performances. However, their prowess is not due only to the improvements in their architecture and training algorithms but also to a drastic increase in computational power used to train them. Such a drastic increase led to a growing interest in distributed ML, which in turn made worker failures and adversarial attacks an increasingly pressing concern. While distributed byzantine resilient algorithms have been proposed in a differentiable setting, none exist in a gradient-free setting. The goal of this work is to address this shortcoming. For that, we introduce a more general definition of byzantine-resilience in ML - the \textit{model-consensus}, that extends the definition of the classical distributed consensus. We then leverage this definition to show that a general class of gradient-free ML algorithms - ($1,\lambda$)-Evolutionary Search - can be combined with classical distributed consensus algorithms to generate gradient-free byzantine-resilient distributed learning algorithms. We provide proofs and pseudo-code for two specific cases - the Total Order Broadcast and proof-of-work leader election.