Matt Gormley
Autoregressive Modeling is Misspecified for Some Sequence Distributions
Oct 22, 2020
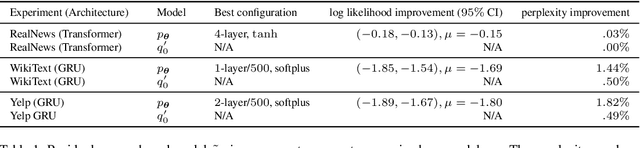


Abstract:Should sequences be modeled autoregressively---one symbol at a time? How much computation is needed to predict the next symbol? While local normalization is cheap, this also limits its power. We point out that some probability distributions over discrete sequences cannot be well-approximated by any autoregressive model whose runtime and parameter size grow polynomially in the sequence length---even though their unnormalized sequence probabilities are efficient to compute exactly. Intuitively, the probability of the next symbol can be expensive to compute or approximate (even via randomized algorithms) when it marginalizes over exponentially many possible futures, which is in general $\mathrm{NP}$-hard. Our result is conditional on the widely believed hypothesis that $\mathrm{NP} \nsubseteq \mathrm{P/poly}$ (without which the polynomial hierarchy would collapse at the second level). This theoretical observation serves as a caution to the viewpoint that pumping up parameter size is a straightforward way to improve autoregressive models (e.g., in language modeling). It also suggests that globally normalized (energy-based) models may sometimes outperform locally normalized (autoregressive) models, as we demonstrate experimentally for language modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge