Is the U-Net Directional-Relationship Aware?

CNNs are often assumed to be capable of using contextual information about distinct objects (such as their directional relations) inside their receptive field. However, the nature and limits of this capacity has never been explored in full. We explore a specific type of relationship~-- directional~-- using a standard U-Net trained to optimize a cross-entropy loss function for segmentation. We train this network on a pretext segmentation task requiring directional relation reasoning for success and state that, with enough data and a sufficiently large receptive field, it succeeds to learn the proposed task. We further explore what the network has learned by analysing scenarios where the directional relationships are perturbed, and show that the network has learned to reason using these relationships.

Template-Based Graph Clustering

We propose a novel graph clustering method guided by additional information on the underlying structure of the clusters (or communities). The problem is formulated as the matching of a graph to a template with smaller dimension, hence matching $n$ vertices of the observed graph (to be clustered) to the $k$ vertices of a template graph, using its edges as support information, and relaxed on the set of orthonormal matrices in order to find a $k$ dimensional embedding. With relevant priors that encode the density of the clusters and their relationships, our method outperforms classical methods, especially for challenging cases.

Approximation of dilation-based spatial relations to add structural constraints in neural networks

Spatial relations between objects in an image have proved useful for structural object recognition. Structural constraints can act as regularization in neural network training, improving generalization capability with small datasets. Several relations can be modeled as a morphological dilation of a reference object with a structuring element representing the semantics of the relation, from which the degree of satisfaction of the relation between another object and the reference object can be derived. However, dilation is not differentiable, requiring an approximation to be used in the context of gradient-descent training of a network. We propose to approximate dilations using convolutions based on a kernel equal to the structuring element. We show that the proposed approximation, even if slightly less accurate than previous approximations, is definitely faster to compute and therefore more suitable for computationally intensive neural network applications.

A Structural Graph-Based Method for MRI Analysis

The importance of imaging exams, such as Magnetic Resonance Imaging (MRI), for the diagnostic and follow-up of pediatric pathologies and the assessment of anatomical structures' development has been increasingly highlighted in recent times. Manual analysis of MRIs is time-consuming, subjective, and requires significant expertise. To mitigate this, automatic techniques are necessary. Most techniques focus on adult subjects, while pediatric MRI has specific challenges such as the ongoing anatomical and histological changes related to normal development of the organs, reduced signal-to-noise ratio due to the smaller bodies, motion artifacts and cooperation issues, especially in long exams, which can in many cases preclude common analysis methods developed for use in adults. Therefore, the development of a robust technique to aid in pediatric MRI analysis is necessary. This paper presents the current development of a new method based on the learning and matching of structural relational graphs (SRGs). The experiments were performed on liver MRI sequences of one patient from ICr-HC-FMUSP, and preliminary results showcased the viability of the project. Future experiments are expected to culminate with an application for pediatric liver substructure and brain tumor segmentation.

An incremental linear-time learning algorithm for the Optimum-Path Forest classifier

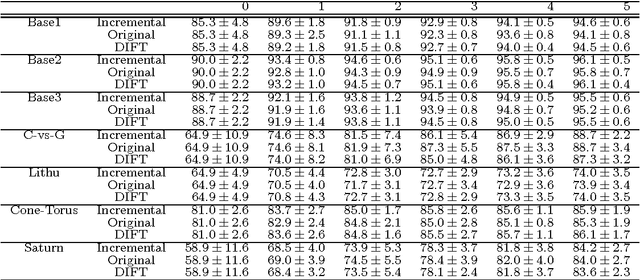
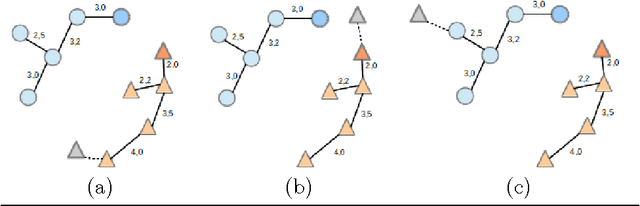
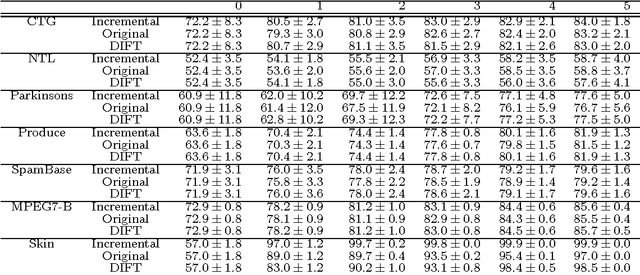
We present a classification method with incremental capabilities based on the Optimum-Path Forest classifier (OPF). The OPF considers instances as nodes of a fully-connected training graph, arc weights represent distances between two feature vectors. Our algorithm includes new instances in an OPF in linear-time, while keeping similar accuracies when compared with the original quadratic-time model.