Regression Trees for Fast and Adaptive Prediction Intervals

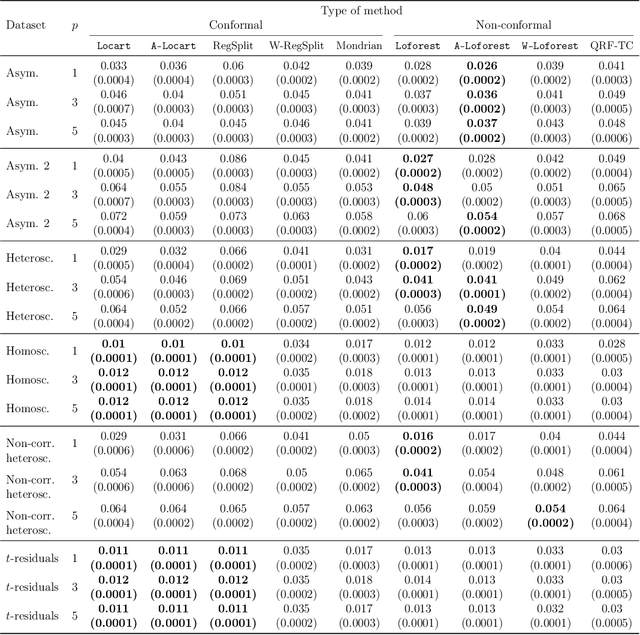
Predictive models make mistakes. Hence, there is a need to quantify the uncertainty associated with their predictions. Conformal inference has emerged as a powerful tool to create statistically valid prediction regions around point predictions, but its naive application to regression problems yields non-adaptive regions. New conformal scores, often relying upon quantile regressors or conditional density estimators, aim to address this limitation. Although they are useful for creating prediction bands, these scores are detached from the original goal of quantifying the uncertainty around an arbitrary predictive model. This paper presents a new, model-agnostic family of methods to calibrate prediction intervals for regression problems with local coverage guarantees. Our approach is based on pursuing the coarsest partition of the feature space that approximates conditional coverage. We create this partition by training regression trees and Random Forests on conformity scores. Our proposal is versatile, as it applies to various conformity scores and prediction settings and demonstrates superior scalability and performance compared to established baselines in simulated and real-world datasets. We provide a Python package clover that implements our methods using the standard scikit-learn interface.

RFFNet: Scalable and interpretable kernel methods via Random Fourier Features

Kernel methods provide a flexible and theoretically grounded approach to nonlinear and nonparametric learning. While memory requirements hinder their applicability to large datasets, many approximate solvers were recently developed for scaling up kernel methods, such as random Fourier features. However, these scalable approaches are based on approximations of isotropic kernels, which are incapable of removing the influence of possibly irrelevant features. In this work, we design random Fourier features for automatic relevance determination kernels, widely used for variable selection, and propose a new method based on joint optimization of the kernel machine parameters and the kernel relevances. Additionally, we present a new optimization algorithm that efficiently tackles the resulting objective function, which is non-convex. Numerical validation on synthetic and real-world data shows that our approach achieves low prediction error and effectively identifies relevant predictors. Our solution is modular and uses the PyTorch framework.