Regression Trees for Fast and Adaptive Prediction Intervals
Paper and Code
Feb 13, 2024
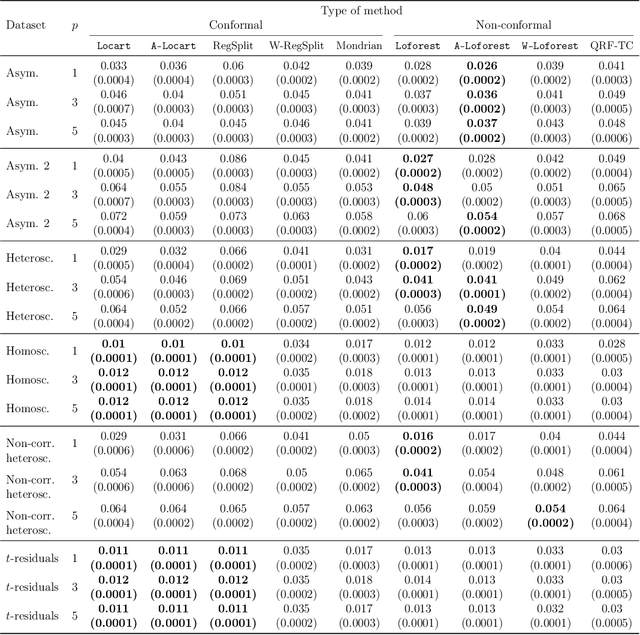


Predictive models make mistakes. Hence, there is a need to quantify the uncertainty associated with their predictions. Conformal inference has emerged as a powerful tool to create statistically valid prediction regions around point predictions, but its naive application to regression problems yields non-adaptive regions. New conformal scores, often relying upon quantile regressors or conditional density estimators, aim to address this limitation. Although they are useful for creating prediction bands, these scores are detached from the original goal of quantifying the uncertainty around an arbitrary predictive model. This paper presents a new, model-agnostic family of methods to calibrate prediction intervals for regression problems with local coverage guarantees. Our approach is based on pursuing the coarsest partition of the feature space that approximates conditional coverage. We create this partition by training regression trees and Random Forests on conformity scores. Our proposal is versatile, as it applies to various conformity scores and prediction settings and demonstrates superior scalability and performance compared to established baselines in simulated and real-world datasets. We provide a Python package clover that implements our methods using the standard scikit-learn interface.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge