Distribution-Free Calibration of Statistical Confidence Sets

Constructing valid confidence sets is a crucial task in statistical inference, yet traditional methods often face challenges when dealing with complex models or limited observed sample sizes. These challenges are frequently encountered in modern applications, such as Likelihood-Free Inference (LFI). In these settings, confidence sets may fail to maintain a confidence level close to the nominal value. In this paper, we introduce two novel methods, TRUST and TRUST++, for calibrating confidence sets to achieve distribution-free conditional coverage. These methods rely entirely on simulated data from the statistical model to perform calibration. Leveraging insights from conformal prediction techniques adapted to the statistical inference context, our methods ensure both finite-sample local coverage and asymptotic conditional coverage as the number of simulations increases, even if n is small. They effectively handle nuisance parameters and provide computationally efficient uncertainty quantification for the estimated confidence sets. This allows users to assess whether additional simulations are necessary for robust inference. Through theoretical analysis and experiments on models with both tractable and intractable likelihoods, we demonstrate that our methods outperform existing approaches, particularly in small-sample regimes. This work bridges the gap between conformal prediction and statistical inference, offering practical tools for constructing valid confidence sets in complex models.

Regression Trees for Fast and Adaptive Prediction Intervals

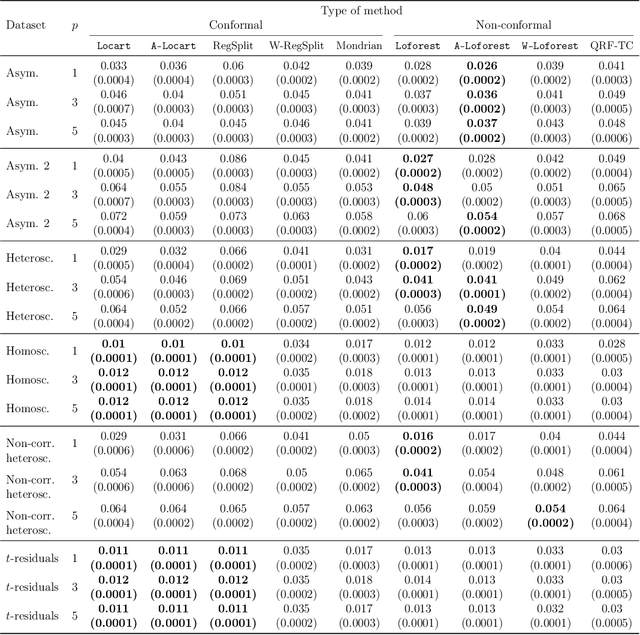
Predictive models make mistakes. Hence, there is a need to quantify the uncertainty associated with their predictions. Conformal inference has emerged as a powerful tool to create statistically valid prediction regions around point predictions, but its naive application to regression problems yields non-adaptive regions. New conformal scores, often relying upon quantile regressors or conditional density estimators, aim to address this limitation. Although they are useful for creating prediction bands, these scores are detached from the original goal of quantifying the uncertainty around an arbitrary predictive model. This paper presents a new, model-agnostic family of methods to calibrate prediction intervals for regression problems with local coverage guarantees. Our approach is based on pursuing the coarsest partition of the feature space that approximates conditional coverage. We create this partition by training regression trees and Random Forests on conformity scores. Our proposal is versatile, as it applies to various conformity scores and prediction settings and demonstrates superior scalability and performance compared to established baselines in simulated and real-world datasets. We provide a Python package clover that implements our methods using the standard scikit-learn interface.

Hierarchical clustering: visualization, feature importance and model selection

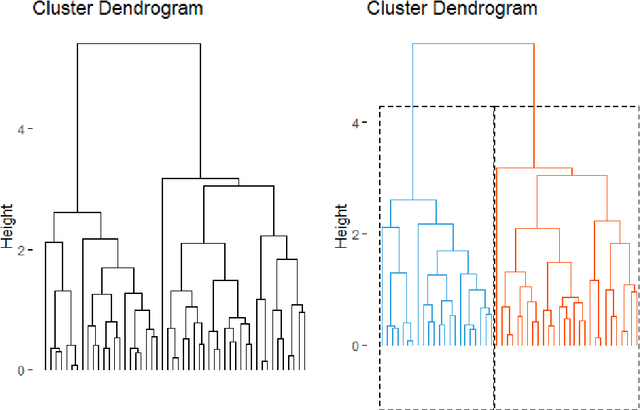
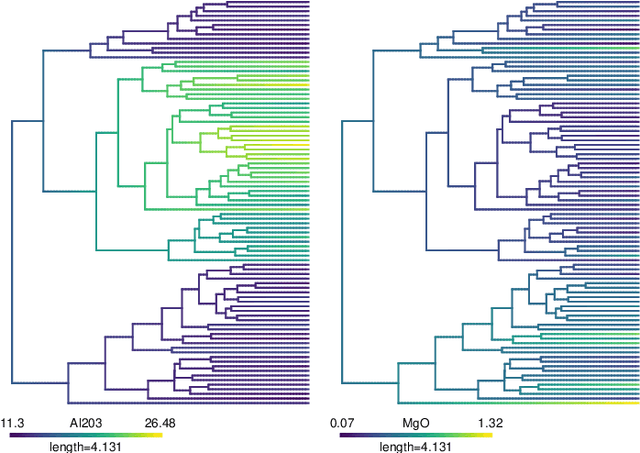
We propose methods for the analysis of hierarchical clustering that fully use the multi-resolution structure provided by a dendrogram. Specifically, we propose a loss for choosing between clustering methods, a feature importance score and a graphical tool for visualizing the segmentation of features in a dendrogram. Current approaches to these tasks lead to loss of information since they require the user to generate a single partition of the instances by cutting the dendrogram at a specified level. Our proposed methods, instead, use the full structure of the dendrogram. The key insight behind the proposed methods is to view a dendrogram as a phylogeny. This analogy permits the assignment of a feature value to each internal node of a tree through ancestral state reconstruction. Real and simulated datasets provide evidence that our proposed framework has desirable outcomes. We provide an R package that implements our methods.