Rethinking Optimal Verification Granularity for Compute-Efficient Test-Time Scaling

Test-time scaling (TTS) has proven effective in enhancing the reasoning capabilities of large language models (LLMs). Verification plays a key role in TTS, simultaneously influencing (1) reasoning performance and (2) compute efficiency, due to the quality and computational cost of verification. In this work, we challenge the conventional paradigms of verification, and make the first attempt toward systematically investigating the impact of verification granularity-that is, how frequently the verifier is invoked during generation, beyond verifying only the final output or individual generation steps. To this end, we introduce Variable Granularity Search (VG-Search), a unified algorithm that generalizes beam search and Best-of-N sampling via a tunable granularity parameter g. Extensive experiments with VG-Search under varying compute budgets, generator-verifier configurations, and task attributes reveal that dynamically selecting g can improve the compute efficiency and scaling behavior. Building on these findings, we propose adaptive VG-Search strategies that achieve accuracy gains of up to 3.1\% over Beam Search and 3.6\% over Best-of-N, while reducing FLOPs by over 52\%. We will open-source the code to support future research.

Annealed Mean Field Descent Is Highly Effective for Quadratic Unconstrained Binary Optimization

In recent years, formulating various combinatorial optimization problems as Quadratic Unconstrained Binary Optimization (QUBO) has gained significant attention as a promising approach for efficiently obtaining optimal or near-optimal solutions. While QUBO offers a general-purpose framework, existing solvers often struggle with performance variability across different problems. This paper (i) theoretically analyzes Mean Field Annealing (MFA) and its variants--which are representative QUBO solvers, and reveals that their underlying self-consistent equations do not necessarily represent the minimum condition of the Kullback-Leibler divergence between the mean-field approximated distribution and the exact distribution, and (ii) proposes a novel method, the Annealed Mean Field Descent (AMFD), which is designed to address this limitation by directly minimizing the divergence. Through extensive experiments on five benchmark combinatorial optimization problems (Maximum Cut Problem, Maximum Independent Set Problem, Traveling Salesman Problem, Quadratic Assignment Problem, and Graph Coloring Problem), we demonstrate that AMFD exhibits superior performance in many cases and reduced problem dependence compared to state-of-the-art QUBO solvers and Gurobi--a state-of-the-art versatile mathematical optimization solver not limited to QUBO.

Partial Search in a Frozen Network is Enough to Find a Strong Lottery Ticket

Randomly initialized dense networks contain subnetworks that achieve high accuracy without weight learning -- strong lottery tickets (SLTs). Recently, Gadhikar et al. (2023) demonstrated theoretically and experimentally that SLTs can also be found within a randomly pruned source network, thus reducing the SLT search space. However, this limits the search to SLTs that are even sparser than the source, leading to worse accuracy due to unintentionally high sparsity. This paper proposes a method that reduces the SLT search space by an arbitrary ratio that is independent of the desired SLT sparsity. A random subset of the initial weights is excluded from the search space by freezing it -- i.e., by either permanently pruning them or locking them as a fixed part of the SLT. Indeed, the SLT existence in such a reduced search space is theoretically guaranteed by our subset-sum approximation with randomly frozen variables. In addition to reducing search space, the random freezing pattern can also be exploited to reduce model size in inference. Furthermore, experimental results show that the proposed method finds SLTs with better accuracy and model size trade-off than the SLTs obtained from dense or randomly pruned source networks. In particular, the SLT found in a frozen graph neural network achieves higher accuracy than its weight trained counterpart while reducing model size by $40.3\times$.

Multicoated and Folded Graph Neural Networks with Strong Lottery Tickets

The Strong Lottery Ticket Hypothesis (SLTH) demonstrates the existence of high-performing subnetworks within a randomly initialized model, discoverable through pruning a convolutional neural network (CNN) without any weight training. A recent study, called Untrained GNNs Tickets (UGT), expanded SLTH from CNNs to shallow graph neural networks (GNNs). However, discrepancies persist when comparing baseline models with learned dense weights. Additionally, there remains an unexplored area in applying SLTH to deeper GNNs, which, despite delivering improved accuracy with additional layers, suffer from excessive memory requirements. To address these challenges, this work utilizes Multicoated Supermasks (M-Sup), a scalar pruning mask method, and implements it in GNNs by proposing a strategy for setting its pruning thresholds adaptively. In the context of deep GNNs, this research uncovers the existence of untrained recurrent networks, which exhibit performance on par with their trained feed-forward counterparts. This paper also introduces the Multi-Stage Folding and Unshared Masks methods to expand the search space in terms of both architecture and parameters. Through the evaluation of various datasets, including the Open Graph Benchmark (OGB), this work establishes a triple-win scenario for SLTH-based GNNs: by achieving high sparsity, competitive performance, and high memory efficiency with up to 98.7\% reduction, it demonstrates suitability for energy-efficient graph processing.

Hidden-Fold Networks: Random Recurrent Residuals Using Sparse Supermasks

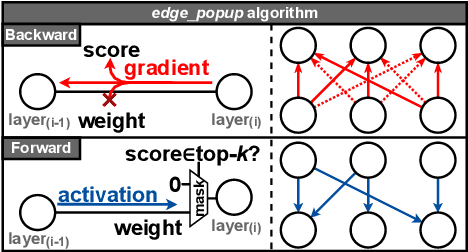
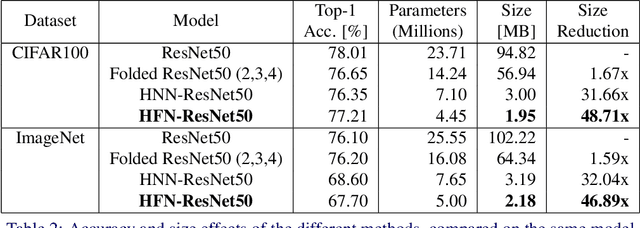
Deep neural networks (DNNs) are so over-parametrized that recent research has found them to already contain a subnetwork with high accuracy at their randomly initialized state. Finding these subnetworks is a viable alternative training method to weight learning. In parallel, another line of work has hypothesized that deep residual networks (ResNets) are trying to approximate the behaviour of shallow recurrent neural networks (RNNs) and has proposed a way for compressing them into recurrent models. This paper proposes blending these lines of research into a highly compressed yet accurate model: Hidden-Fold Networks (HFNs). By first folding ResNet into a recurrent structure and then searching for an accurate subnetwork hidden within the randomly initialized model, a high-performing yet tiny HFN is obtained without ever updating the weights. As a result, HFN achieves equivalent performance to ResNet50 on CIFAR100 while occupying 38.5x less memory, and similar performance to ResNet34 on ImageNet with a memory size 26.8x smaller. The HFN will become even more attractive by minimizing data transfers while staying accurate when it runs on highly-quantized and randomly-weighted DNN inference accelerators. Code available at https://github.com/Lopez-Angel/hidden-fold-networks