One-shot backpropagation for multi-step prediction in physics-based system identification -- EXTENDED VERSION

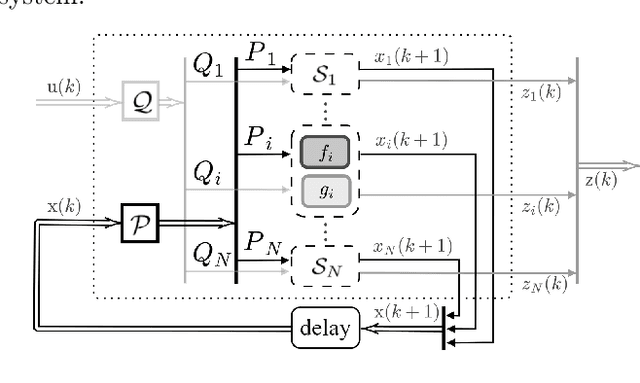
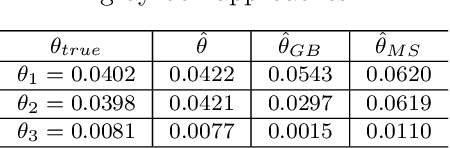
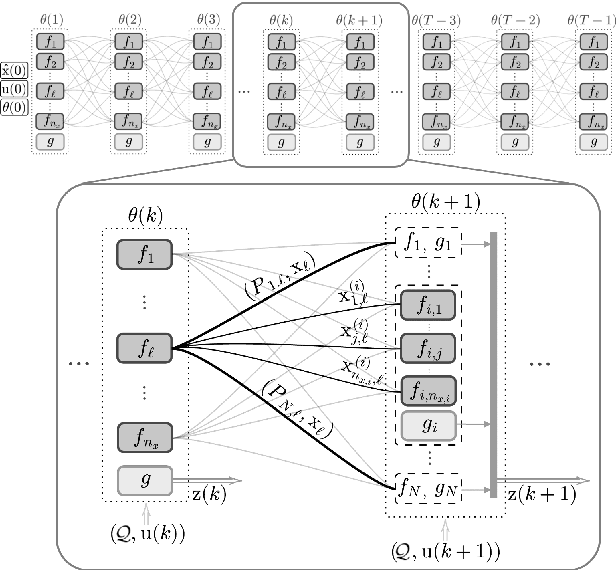
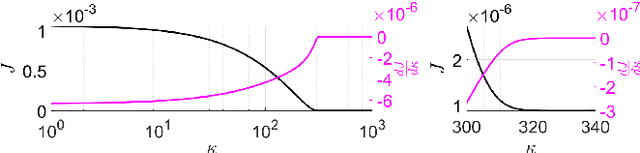
The aim of this paper is to present a novel physics-based framework for the identification of dynamical systems, in which the physical and structural insights are reflected directly into a backpropagation-based learning algorithm. The main result is a method to compute in closed form the gradient of a multi-step loss function, while enforcing physical properties and constraints. The derived algorithm has been exploited to identify the unknown inertia matrix of a space debris, and the results show the reliability of the method in capturing the physical adherence of the estimated parameters.

3D Map Reconstruction of an Orchard using an Angle-Aware Covering Control Strategy

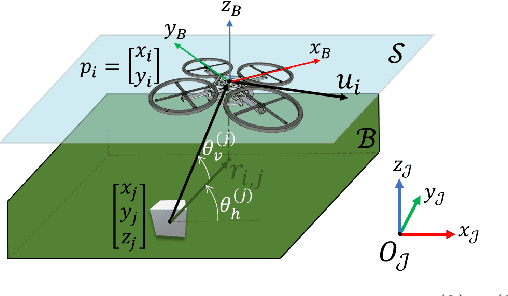
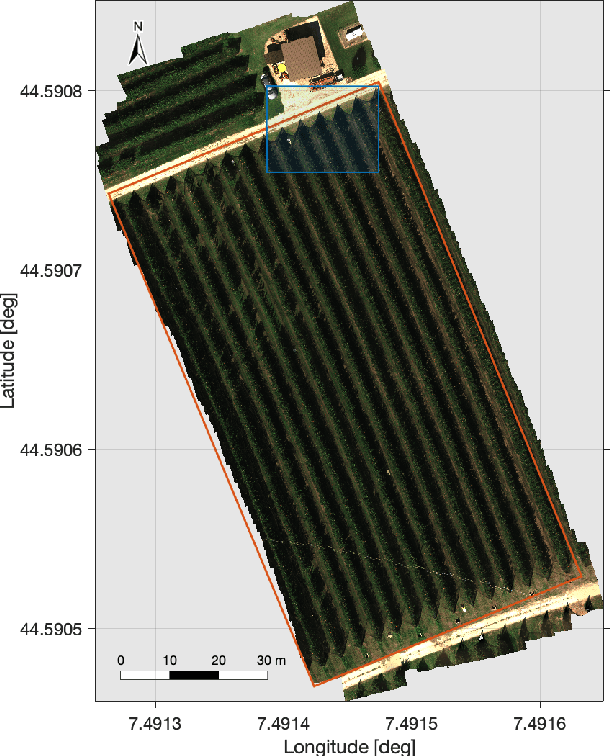
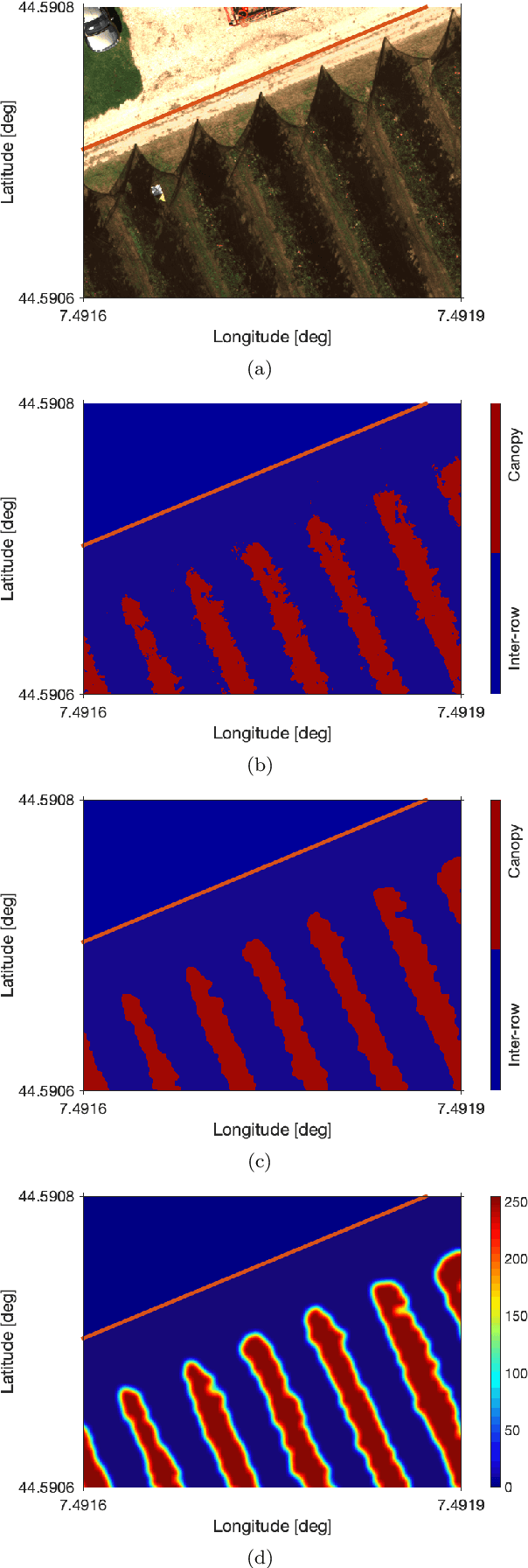
In the last years, unmanned aerial vehicles are becoming a reality in the context of precision agriculture, mainly for monitoring, patrolling and remote sensing tasks, but also for 3D map reconstruction. In this paper, we present an innovative approach where a fleet of unmanned aerial vehicles is exploited to perform remote sensing tasks over an apple orchard for reconstructing a 3D map of the field, formulating the covering control problem to combine the position of a monitoring target and the viewing angle. Moreover, the objective function of the controller is defined by an importance index, which has been computed from a multi-spectral map of the field, obtained by a preliminary flight, using a semantic interpretation scheme based on a convolutional neural network. This objective function is then updated according to the history of the past coverage states, thus allowing the drones to take situation-adaptive actions. The effectiveness of the proposed covering control strategy has been validated through simulations on a Robot Operating System.

Computationally efficient stochastic MPC: a probabilistic scaling approach

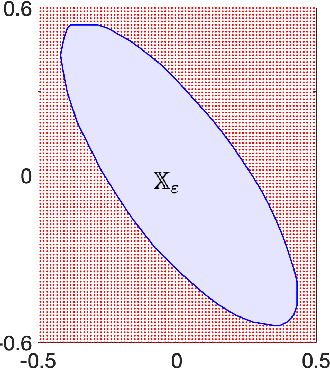
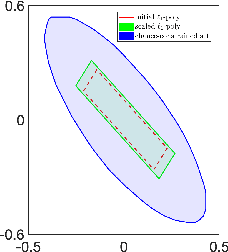
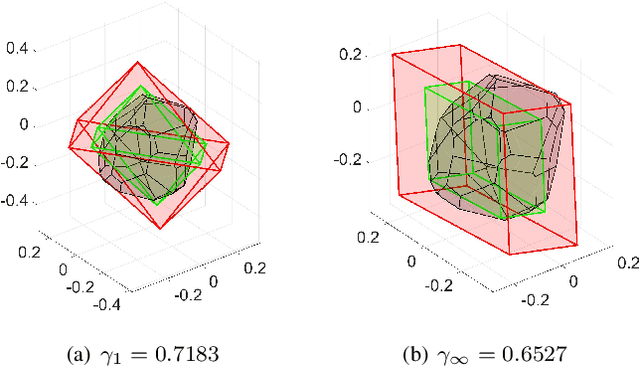
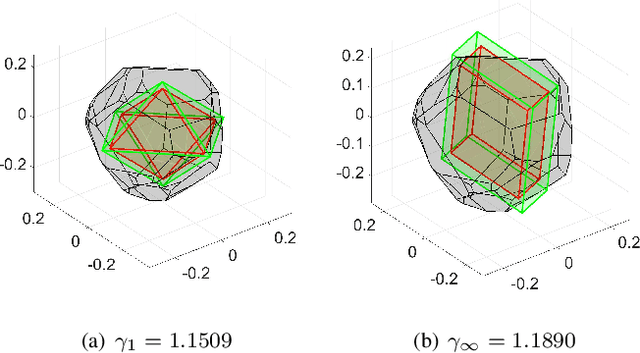
In recent years, the increasing interest in Stochastic model predictive control (SMPC) schemes has highlighted the limitation arising from their inherent computational demand, which has restricted their applicability to slow-dynamics and high-performing systems. To reduce the computational burden, in this paper we extend the probabilistic scaling approach to obtain low-complexity inner approximation of chance-constrained sets. This approach provides probabilistic guarantees at a lower computational cost than other schemes for which the sample complexity depends on the design space dimension. To design candidate simple approximating sets, which approximate the shape of the probabilistic set, we introduce two possibilities: i) fixed-complexity polytopes, and ii) $\ell_p$-norm based sets. Once the candidate approximating set is obtained, it is scaled around its center so to enforce the expected probabilistic guarantees. The resulting scaled set is then exploited to enforce constraints in the classical SMPC framework. The computational gain obtained with the proposed approach with respect to the scenario one is demonstrated via simulations, where the objective is the control of a fixed-wing UAV performing a monitoring mission over a sloped vineyard.

Open Data Resources for Fighting COVID-19

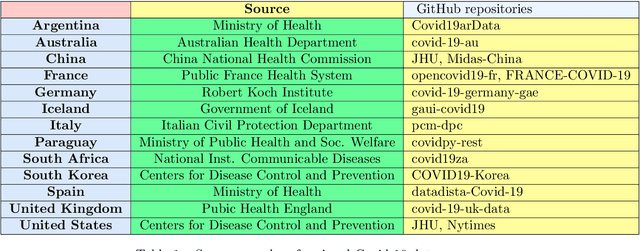
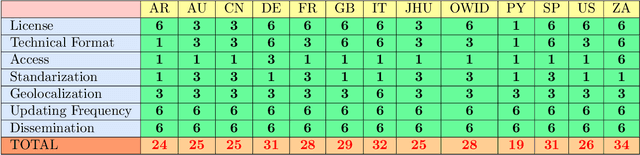
We provide an insight into the open data resources pertinent to the study of the spread of Covid-19 pandemic and its control. We identify the variables required to analyze fundamental aspects like seasonal behaviour, regional mortality rates, and effectiveness of government measures. Open data resources, along with data-driven methodologies, provide many opportunities to improve the response of the different administrations to the virus. We describe the present limitations and difficulties encountered in most of the open-data resources. To facilitate the access to the main open-data portals and resources, we identify the most relevant institutions, at a world scale, providing Covid-19 information and/or auxiliary variables (demographics, mobility, etc.). We also describe several open resources to access Covid-19 data-sets at a country-wide level (i.e. China, Italy, Spain, France, Germany, U.S., etc.). In an attempt to facilitate the rapid response to the study of the seasonal behaviour of Covid-19, we enumerate the main open resources in terms of weather and climate variables. CONCO-Team: The authors of this paper belong to the CONtrol COvid-19 Team, which is composed of different researches from universities of Spain, Italy, France, Germany, United Kingdom and Argentina. The main goal of CONCO-Team is to develop data-driven methods for the better understanding and control of the pandemic.