Computationally efficient stochastic MPC: a probabilistic scaling approach
Paper and Code
May 21, 2020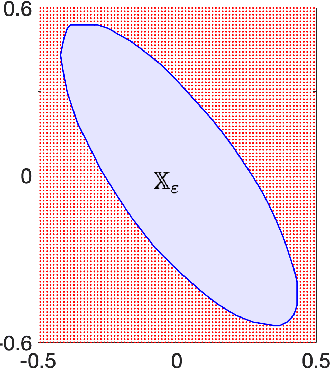
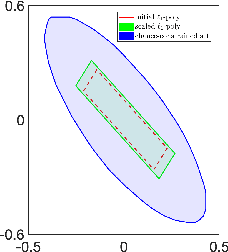
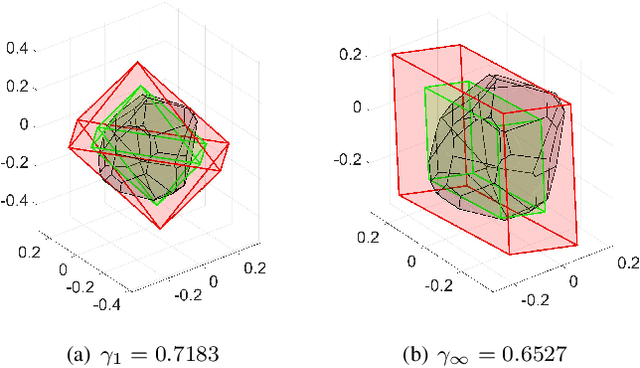
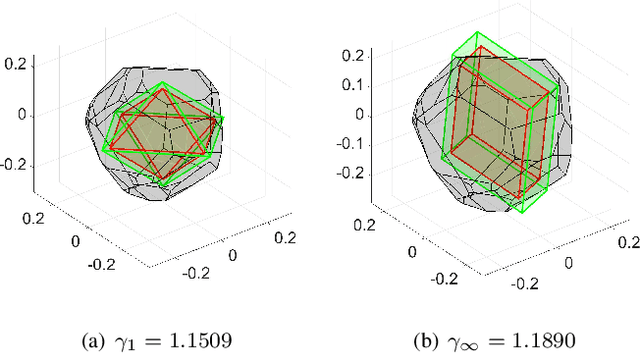
In recent years, the increasing interest in Stochastic model predictive control (SMPC) schemes has highlighted the limitation arising from their inherent computational demand, which has restricted their applicability to slow-dynamics and high-performing systems. To reduce the computational burden, in this paper we extend the probabilistic scaling approach to obtain low-complexity inner approximation of chance-constrained sets. This approach provides probabilistic guarantees at a lower computational cost than other schemes for which the sample complexity depends on the design space dimension. To design candidate simple approximating sets, which approximate the shape of the probabilistic set, we introduce two possibilities: i) fixed-complexity polytopes, and ii) $\ell_p$-norm based sets. Once the candidate approximating set is obtained, it is scaled around its center so to enforce the expected probabilistic guarantees. The resulting scaled set is then exploited to enforce constraints in the classical SMPC framework. The computational gain obtained with the proposed approach with respect to the scenario one is demonstrated via simulations, where the objective is the control of a fixed-wing UAV performing a monitoring mission over a sloped vineyard.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge