Learning Semi-Structured Representations of Radiology Reports

Beyond their primary diagnostic purpose, radiology reports have been an invaluable source of information in medical research. Given a corpus of radiology reports, researchers are often interested in identifying a subset of reports describing a particular medical finding. Because the space of medical findings in radiology reports is vast and potentially unlimited, recent studies proposed mapping free-text statements in radiology reports to semi-structured strings of terms taken from a limited vocabulary. This paper aims to present an approach for the automatic generation of semi-structured representations of radiology reports. The approach consists of matching sentences from radiology reports to manually created semi-structured representations, followed by learning a sequence-to-sequence neural model that maps matched sentences to their semi-structured representations. We evaluated the proposed approach on the OpenI corpus of manually annotated chest x-ray radiology reports. The results indicate that the proposed approach is superior to several baselines, both in terms of (1) quantitative measures such as BLEU, ROUGE, and METEOR and (2) qualitative judgment of a radiologist. The results also demonstrate that the trained model produces reasonable semi-structured representations on an out-of-sample corpus of chest x-ray radiology reports from a different medical provider.

Stability of decision trees and logistic regression

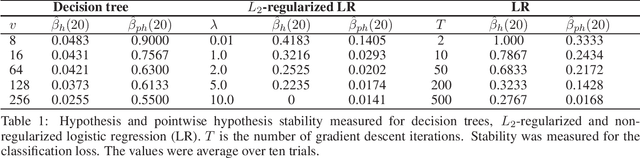
Decision trees and logistic regression are one of the most popular and well-known machine learning algorithms, frequently used to solve a variety of real-world problems. Stability of learning algorithms is a powerful tool to analyze their performance and sensitivity and subsequently allow researchers to draw reliable conclusions. The stability of these two algorithms has remained obscure. To that end, in this paper, we derive two stability notions for decision trees and logistic regression: hypothesis and pointwise hypothesis stability. Additionally, we derive these notions for L2-regularized logistic regression and confirm existing findings that it is uniformly stable. We show that the stability of decision trees depends on the number of leaves in the tree, i.e., its depth, while for logistic regression, it depends on the smallest eigenvalue of the Hessian matrix of the cross-entropy loss. We show that logistic regression is not a stable learning algorithm. We construct the upper bounds on the generalization error of all three algorithms. Moreover, we present a novel stability measuring framework that allows one to measure the aforementioned notions of stability. The measures are equivalent to estimates of expected loss differences at an input example and then leverage bootstrap sampling to yield statistically reliable estimates. Finally, we apply this framework to the three algorithms analyzed in this paper to confirm our theoretical findings and, in addition, we discuss the possibilities of developing new training techniques to optimize the stability of logistic regression, and hence decrease its generalization error.

Stacking and stability

Stacking is a general approach for combining multiple models toward greater predictive accuracy. It has found various application across different domains, ensuing from its meta-learning nature. Our understanding, nevertheless, on how and why stacking works remains intuitive and lacking in theoretical insight. In this paper, we use the stability of learning algorithms as an elemental analysis framework suitable for addressing the issue. To this end, we analyze the hypothesis stability of stacking, bag-stacking, and dag-stacking and establish a connection between bag-stacking and weighted bagging. We show that the hypothesis stability of stacking is a product of the hypothesis stability of each of the base models and the combiner. Moreover, in bag-stacking and dag-stacking, the hypothesis stability depends on the sampling strategy used to generate the training set replicates. Our findings suggest that 1) subsampling and bootstrap sampling improve the stability of stacking, and 2) stacking improves the stability of both subbagging and bagging.