Stability of decision trees and logistic regression
Paper and Code
Mar 03, 2019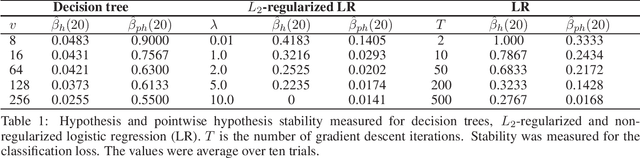
Decision trees and logistic regression are one of the most popular and well-known machine learning algorithms, frequently used to solve a variety of real-world problems. Stability of learning algorithms is a powerful tool to analyze their performance and sensitivity and subsequently allow researchers to draw reliable conclusions. The stability of these two algorithms has remained obscure. To that end, in this paper, we derive two stability notions for decision trees and logistic regression: hypothesis and pointwise hypothesis stability. Additionally, we derive these notions for L2-regularized logistic regression and confirm existing findings that it is uniformly stable. We show that the stability of decision trees depends on the number of leaves in the tree, i.e., its depth, while for logistic regression, it depends on the smallest eigenvalue of the Hessian matrix of the cross-entropy loss. We show that logistic regression is not a stable learning algorithm. We construct the upper bounds on the generalization error of all three algorithms. Moreover, we present a novel stability measuring framework that allows one to measure the aforementioned notions of stability. The measures are equivalent to estimates of expected loss differences at an input example and then leverage bootstrap sampling to yield statistically reliable estimates. Finally, we apply this framework to the three algorithms analyzed in this paper to confirm our theoretical findings and, in addition, we discuss the possibilities of developing new training techniques to optimize the stability of logistic regression, and hence decrease its generalization error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge