Colored Jones Polynomials and the Volume Conjecture

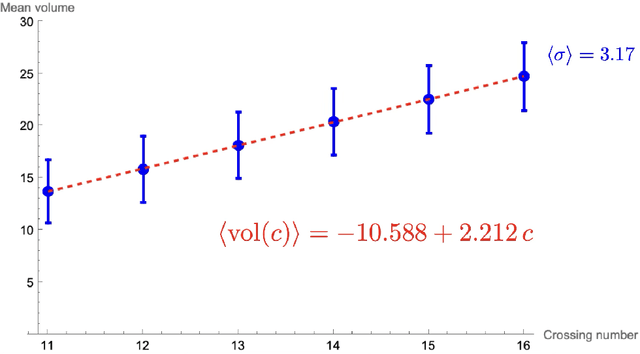
Using the vertex model approach for braid representations, we compute polynomials for spin-1 placed on hyperbolic knots up to 15 crossings. These polynomials are referred to as 3-colored Jones polynomials or adjoint Jones polynomials. Training a subset of the data using a fully connected feedforward neural network, we predict the volume of the knot complement of hyperbolic knots from the adjoint Jones polynomial or its evaluations with 99.34% accuracy. A function of the adjoint Jones polynomial evaluated at the phase $q=e^{ 8 \pi i / 15 }$ predicts the volume with nearly the same accuracy as the neural network. From an analysis of 2-colored and 3-colored Jones polynomials, we conjecture the best phase for $n$-colored Jones polynomials, and use this hypothesis to motivate an improved statement of the volume conjecture. This is tested for knots for which closed form expressions for the $n$-colored Jones polynomial are known, and we show improved convergence to the volume.

Learning knot invariants across dimensions

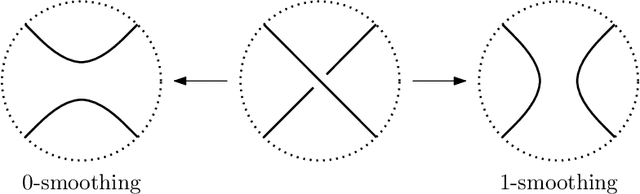
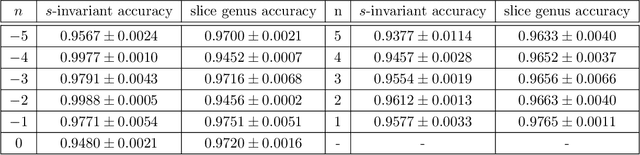
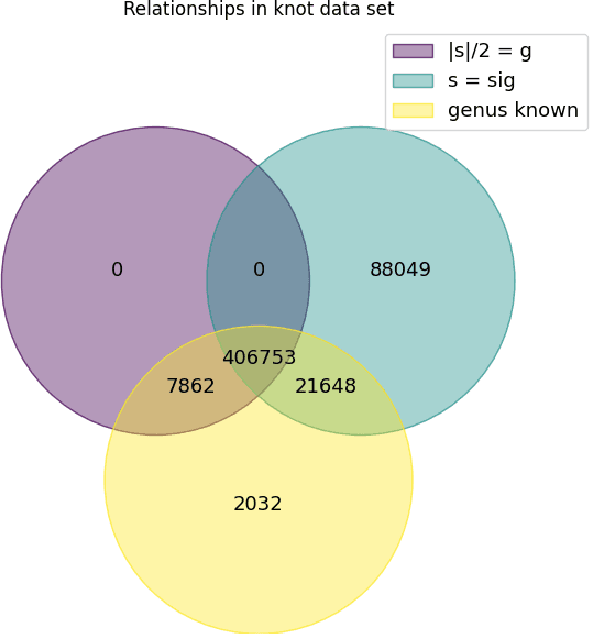
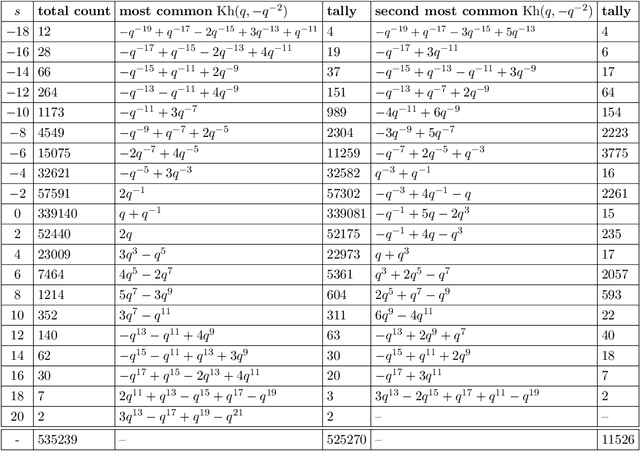
We use deep neural networks to machine learn correlations between knot invariants in various dimensions. The three-dimensional invariant of interest is the Jones polynomial $J(q)$, and the four-dimensional invariants are the Khovanov polynomial $\text{Kh}(q,t)$, smooth slice genus $g$, and Rasmussen's $s$-invariant. We find that a two-layer feed-forward neural network can predict $s$ from $\text{Kh}(q,-q^{-4})$ with greater than $99\%$ accuracy. A theoretical explanation for this performance exists in knot theory via the now disproven knight move conjecture, which is obeyed by all knots in our dataset. More surprisingly, we find similar performance for the prediction of $s$ from $\text{Kh}(q,-q^{-2})$, which suggests a novel relationship between the Khovanov and Lee homology theories of a knot. The network predicts $g$ from $\text{Kh}(q,t)$ with similarly high accuracy, and we discuss the extent to which the machine is learning $s$ as opposed to $g$, since there is a general inequality $|s| \leq 2g$. The Jones polynomial, as a three-dimensional invariant, is not obviously related to $s$ or $g$, but the network achieves greater than $95\%$ accuracy in predicting either from $J(q)$. Moreover, similar accuracy can be achieved by evaluating $J(q)$ at roots of unity. This suggests a relationship with $SU(2)$ Chern--Simons theory, and we review the gauge theory construction of Khovanov homology which may be relevant for explaining the network's performance.

Medical Text Classification using Convolutional Neural Networks

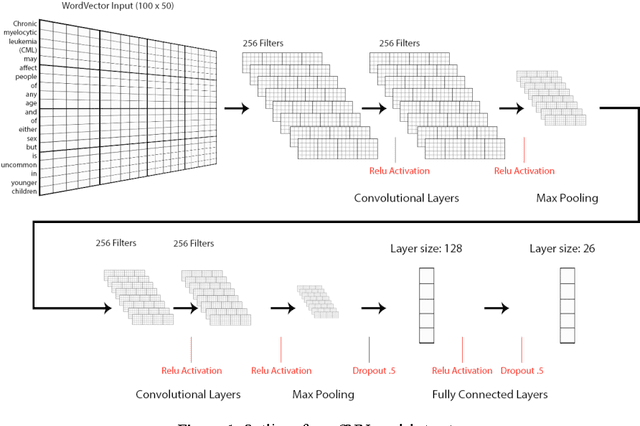
We present an approach to automatically classify clinical text at a sentence level. We are using deep convolutional neural networks to represent complex features. We train the network on a dataset providing a broad categorization of health information. Through a detailed evaluation, we demonstrate that our method outperforms several approaches widely used in natural language processing tasks by about 15%.