Learning knot invariants across dimensions

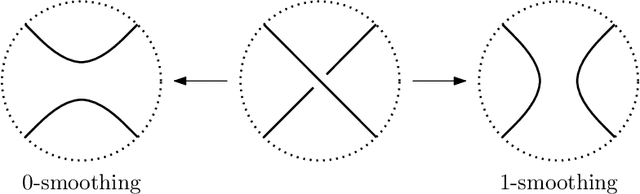
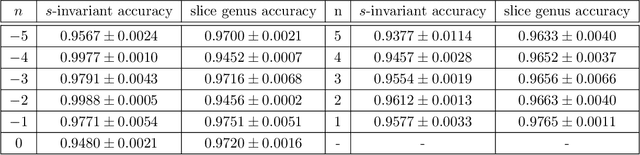
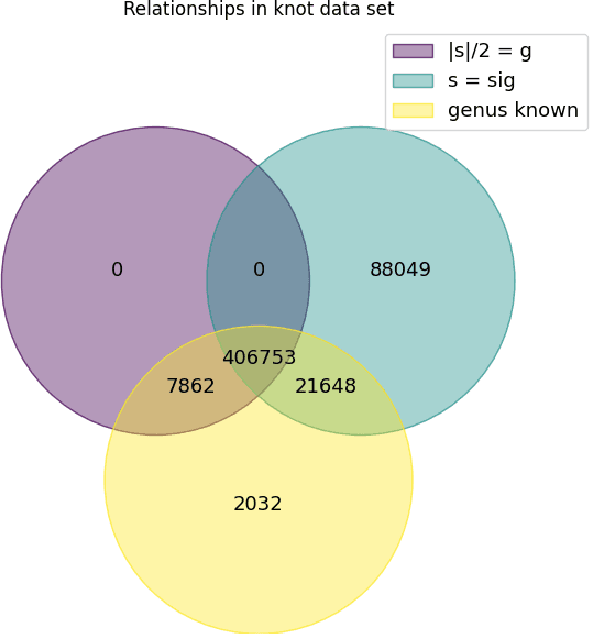
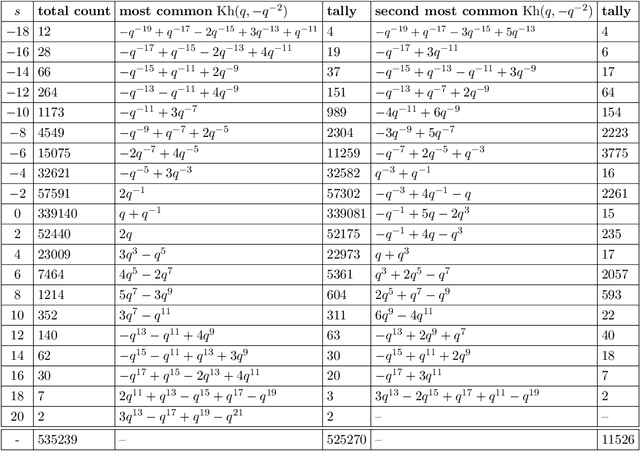
We use deep neural networks to machine learn correlations between knot invariants in various dimensions. The three-dimensional invariant of interest is the Jones polynomial $J(q)$, and the four-dimensional invariants are the Khovanov polynomial $\text{Kh}(q,t)$, smooth slice genus $g$, and Rasmussen's $s$-invariant. We find that a two-layer feed-forward neural network can predict $s$ from $\text{Kh}(q,-q^{-4})$ with greater than $99\%$ accuracy. A theoretical explanation for this performance exists in knot theory via the now disproven knight move conjecture, which is obeyed by all knots in our dataset. More surprisingly, we find similar performance for the prediction of $s$ from $\text{Kh}(q,-q^{-2})$, which suggests a novel relationship between the Khovanov and Lee homology theories of a knot. The network predicts $g$ from $\text{Kh}(q,t)$ with similarly high accuracy, and we discuss the extent to which the machine is learning $s$ as opposed to $g$, since there is a general inequality $|s| \leq 2g$. The Jones polynomial, as a three-dimensional invariant, is not obviously related to $s$ or $g$, but the network achieves greater than $95\%$ accuracy in predicting either from $J(q)$. Moreover, similar accuracy can be achieved by evaluating $J(q)$ at roots of unity. This suggests a relationship with $SU(2)$ Chern--Simons theory, and we review the gauge theory construction of Khovanov homology which may be relevant for explaining the network's performance.

Disentangling a Deep Learned Volume Formula

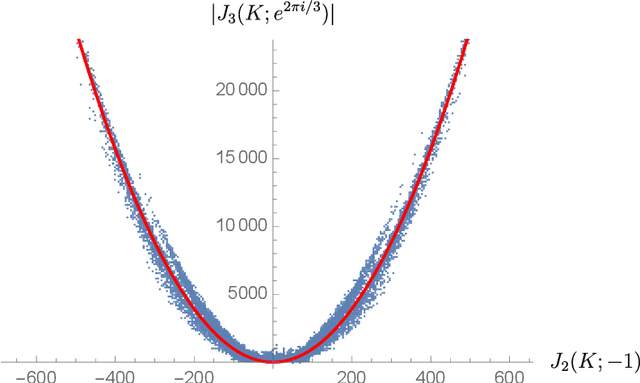
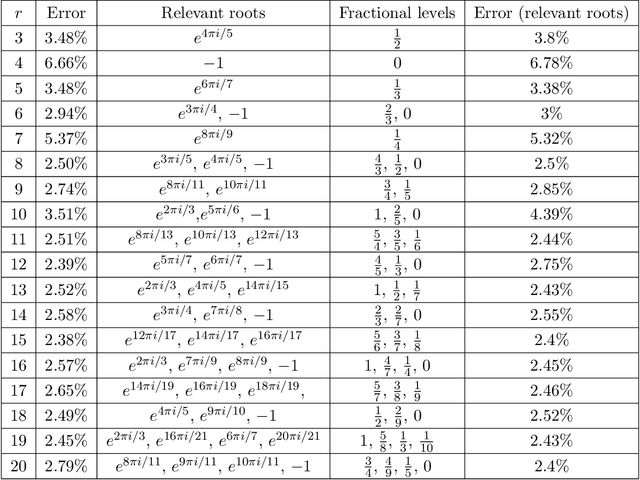
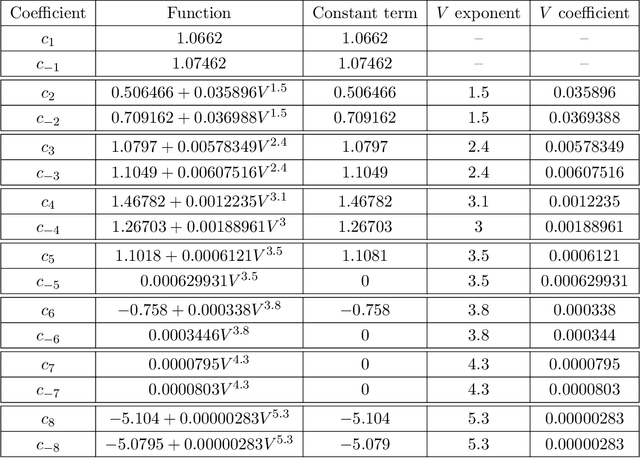
We present a simple phenomenological formula which approximates the hyperbolic volume of a knot using only a single evaluation of its Jones polynomial at a root of unity. The average error is just 2.86% on the first 1.7 million knots, which represents a large improvement over previous formulas of this kind. To find the approximation formula, we use layer-wise relevance propagation to reverse engineer a black box neural network which achieves a similar average error for the same approximation task when trained on 10% of the total dataset. The particular roots of unity which appear in our analysis cannot be written as $e^{2\pi i / (k+2)}$ with integer $k$; therefore, the relevant Jones polynomial evaluations are not given by unknot-normalized expectation values of Wilson loop operators in conventional $SU(2)$ Chern-Simons theory with level $k$. Instead, they correspond to an analytic continuation of such expectation values to fractional level. We briefly review the continuation procedure and comment on the presence of certain Lefschetz thimbles, to which our approximation formula is sensitive, in the analytically continued Chern-Simons integration cycle.