Mark Easton
IT-RUDA: Information Theory Assisted Robust Unsupervised Domain Adaptation
Oct 24, 2022
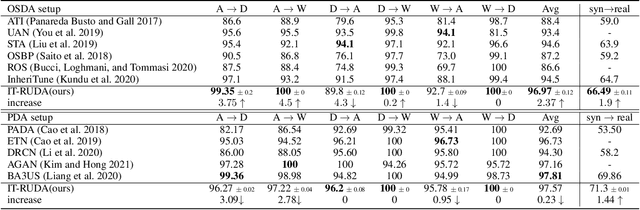

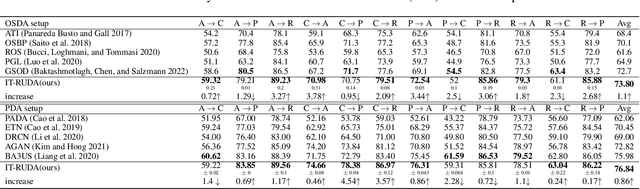
Abstract:Distribution shift between train (source) and test (target) datasets is a common problem encountered in machine learning applications. One approach to resolve this issue is to use the Unsupervised Domain Adaptation (UDA) technique that carries out knowledge transfer from a label-rich source domain to an unlabeled target domain. Outliers that exist in either source or target datasets can introduce additional challenges when using UDA in practice. In this paper, $\alpha$-divergence is used as a measure to minimize the discrepancy between the source and target distributions while inheriting robustness, adjustable with a single parameter $\alpha$, as the prominent feature of this measure. Here, it is shown that the other well-known divergence-based UDA techniques can be derived as special cases of the proposed method. Furthermore, a theoretical upper bound is derived for the loss in the target domain in terms of the source loss and the initial $\alpha$-divergence between the two domains. The robustness of the proposed method is validated through testing on several benchmarked datasets in open-set and partial UDA setups where extra classes existing in target and source datasets are considered as outliers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge