On the design space between molecular mechanics and machine learning force fields

A force field as accurate as quantum mechanics (QM) and as fast as molecular mechanics (MM), with which one can simulate a biomolecular system efficiently enough and meaningfully enough to get quantitative insights, is among the most ardent dreams of biophysicists -- a dream, nevertheless, not to be fulfilled any time soon. Machine learning force fields (MLFFs) represent a meaningful endeavor towards this direction, where differentiable neural functions are parametrized to fit ab initio energies, and furthermore forces through automatic differentiation. We argue that, as of now, the utility of the MLFF models is no longer bottlenecked by accuracy but primarily by their speed (as well as stability and generalizability), as many recent variants, on limited chemical spaces, have long surpassed the chemical accuracy of $1$ kcal/mol -- the empirical threshold beyond which realistic chemical predictions are possible -- though still magnitudes slower than MM. Hoping to kindle explorations and designs of faster, albeit perhaps slightly less accurate MLFFs, in this review, we focus our attention on the design space (the speed-accuracy tradeoff) between MM and ML force fields. After a brief review of the building blocks of force fields of either kind, we discuss the desired properties and challenges now faced by the force field development community, survey the efforts to make MM force fields more accurate and ML force fields faster, envision what the next generation of MLFF might look like.

By-passing the Kohn-Sham equations with machine learning

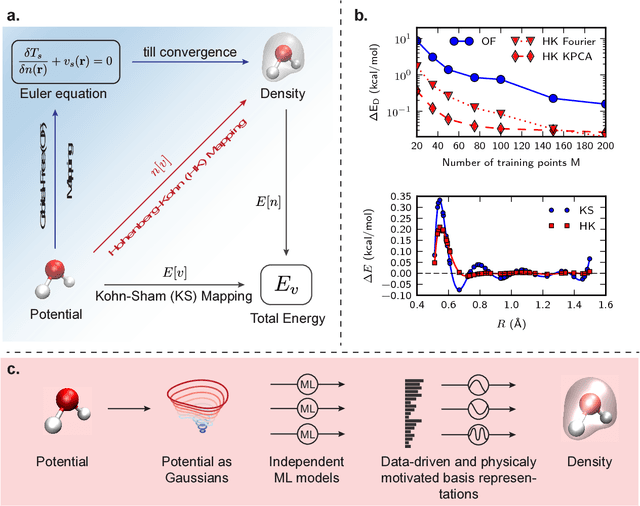
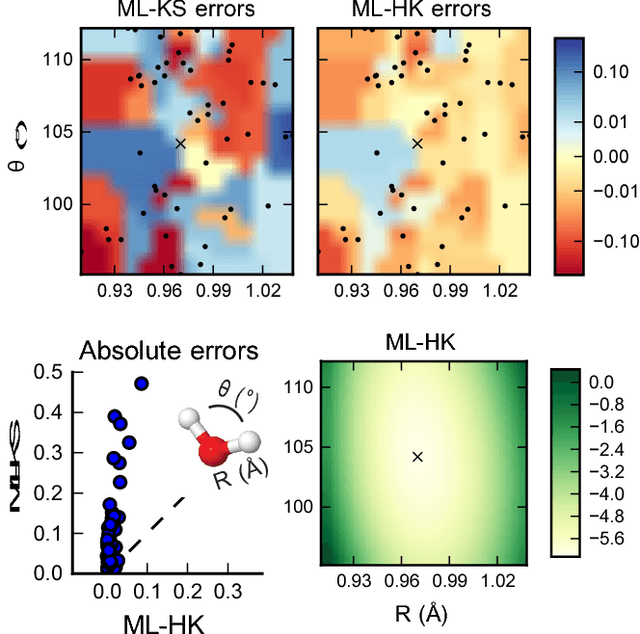
Last year, at least 30,000 scientific papers used the Kohn-Sham scheme of density functional theory to solve electronic structure problems in a wide variety of scientific fields, ranging from materials science to biochemistry to astrophysics. Machine learning holds the promise of learning the kinetic energy functional via examples, by-passing the need to solve the Kohn-Sham equations. This should yield substantial savings in computer time, allowing either larger systems or longer time-scales to be tackled, but attempts to machine-learn this functional have been limited by the need to find its derivative. The present work overcomes this difficulty by directly learning the density-potential and energy-density maps for test systems and various molecules. Both improved accuracy and lower computational cost with this method are demonstrated by reproducing DFT energies for a range of molecular geometries generated during molecular dynamics simulations. Moreover, the methodology could be applied directly to quantum chemical calculations, allowing construction of density functionals of quantum-chemical accuracy.