Testing the Limits of Truth Directions in LLMs

Large language models (LLMs) have been shown to encode truth of statements in their activation space along a linear truth direction. Previous studies have argued that these directions are universal in certain aspects, while more recent work has questioned this conclusion drawing on limited generalization across some settings. In this work, we identify a number of limits of truth-direction universality that have not been previously understood. We first show that truth directions are highly layer-dependent, and that a full understanding of universality requires probing at many layers in the model. We then show that truth directions depend heavily on task type, emerging in earlier layers for factual and later layers for reasoning tasks; they also vary in performance across levels of task complexity. Finally, we show that model instructions dramatically affect truth directions; simple correctness evaluation instructions significantly affect the generalization ability of truth probes. Our findings indicate that universality claims for truth directions are more limited than previously known, with significant differences observable for various model layers, task difficulties, task types, and prompt templates.

Singular Vectors of Attention Heads Align with Features

Identifying feature representations in language models is a central task in mechanistic interpretability. Several recent studies have made an implicit assumption that feature representations can be inferred in some cases from singular vectors of attention matrices. However, sound justification for this assumption is lacking. In this paper we address that question, asking: why and when do singular vectors align with features? First, we demonstrate that singular vectors robustly align with features in a model where features can be directly observed. We then show theoretically that such alignment is expected under a range of conditions. We close by asking how, operationally, alignment may be recognized in real models where feature representations are not directly observable. We identify sparse attention decomposition as a testable prediction of alignment, and show evidence that it emerges in a manner consistent with predictions in real models. Together these results suggest that alignment of singular vectors with features can be a sound and theoretically justified basis for feature identification in language models.

Finding Highly Interpretable Prompt-Specific Circuits in Language Models

Understanding the internal circuits that language models use to solve tasks remains a central challenge in mechanistic interpretability. Most prior work identifies circuits at the task level by averaging across many prompts, implicitly assuming a single stable mechanism per task. We show that this assumption can obscure a crucial source of structure: circuits are prompt-specific, even within a fixed task. Building on attention causal communication (ACC) (Franco & Crovella, 2025), we introduce ACC++, refinements that extract cleaner, lower-dimensional causal signals inside attention heads from a single forward pass. Like ACC, our approach does not require replacement models (e.g., SAEs) or activation patching; ACC++ further improves circuit precision by reducing attribution noise. Applying ACC++ to indirect object identification (IOI) in GPT-2, Pythia, and Gemma 2, we find there is no single circuit for IOI in any model: different prompt templates induce systematically different mechanisms. Despite this variation, prompts cluster into prompt families with similar circuits, and we propose a representative circuit for each family as a practical unit of analysis. Finally, we develop an automated interpretability pipeline that uses ACC++ signals to surface human-interpretable features and assemble mechanistic explanations for prompt families behavior. Together, our results recast circuits as a meaningful object of study by shifting the unit of analysis from tasks to prompts, enabling scalable circuit descriptions in the presence of prompt-specific mechanisms.

Evaluating LLP Methods: Challenges and Approaches

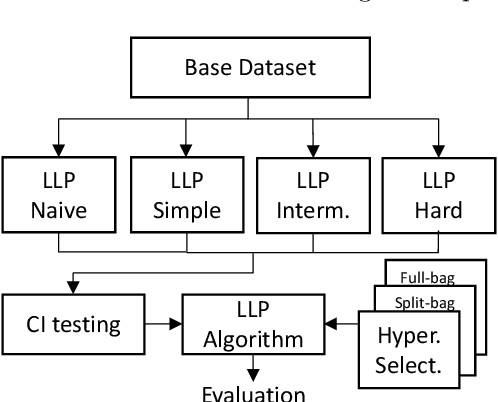
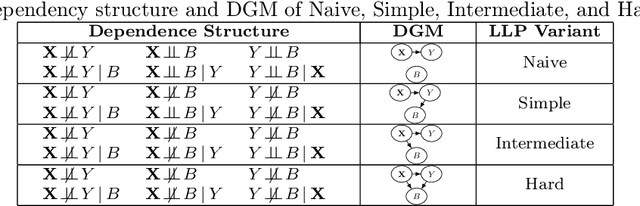
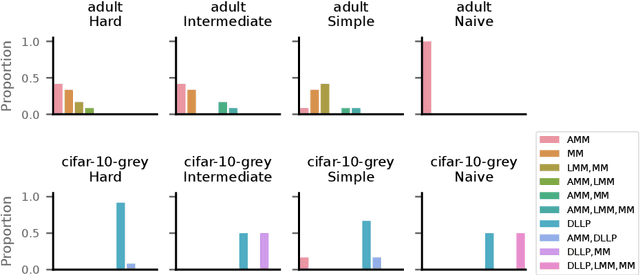
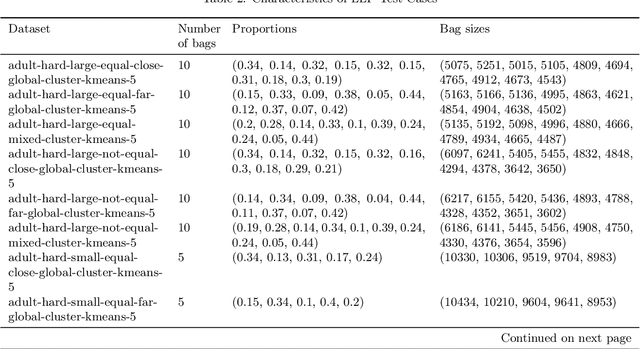
Learning from Label Proportions (LLP) is an established machine learning problem with numerous real-world applications. In this setting, data items are grouped into bags, and the goal is to learn individual item labels, knowing only the features of the data and the proportions of labels in each bag. Although LLP is a well-established problem, it has several unusual aspects that create challenges for benchmarking learning methods. Fundamental complications arise because of the existence of different LLP variants, i.e., dependence structures that can exist between items, labels, and bags. Accordingly, the first algorithmic challenge is the generation of variant-specific datasets capturing the diversity of dependence structures and bag characteristics. The second methodological challenge is model selection, i.e., hyperparameter tuning; due to the nature of LLP, model selection cannot easily use the standard machine learning paradigm. The final benchmarking challenge consists of properly evaluating LLP solution methods across various LLP variants. We note that there is very little consideration of these issues in prior work, and there are no general solutions for these challenges proposed to date. To address these challenges, we develop methods capable of generating LLP datasets meeting the requirements of different variants. We use these methods to generate a collection of datasets encompassing the spectrum of LLP problem characteristics, which can be used in future evaluation studies. Additionally, we develop guidelines for benchmarking LLP algorithms, including the model selection and evaluation steps. Finally, we illustrate the new methods and guidelines by performing an extensive benchmark of a set of well-known LLP algorithms. We show that choosing the best algorithm depends critically on the LLP variant and model selection method, demonstrating the need for our proposed approach.

Fair Inputs and Fair Outputs: The Incompatibility of Fairness in Privacy and Accuracy

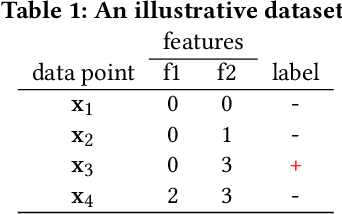
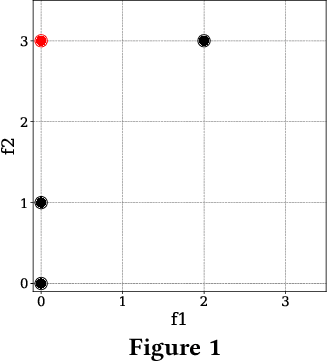
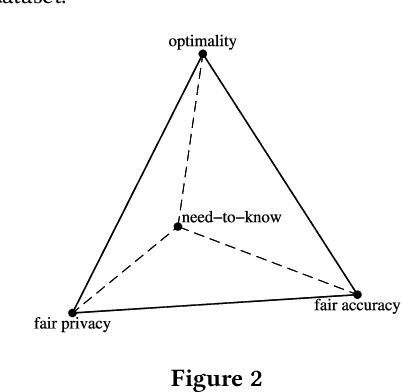
Fairness concerns about algorithmic decision-making systems have been mainly focused on the outputs (e.g., the accuracy of a classifier across individuals or groups). However, one may additionally be concerned with fairness in the inputs. In this paper, we propose and formulate two properties regarding the inputs of (features used by) a classifier. In particular, we claim that fair privacy (whether individuals are all asked to reveal the same information) and need-to-know (whether users are only asked for the minimal information required for the task at hand) are desirable properties of a decision system. We explore the interaction between these properties and fairness in the outputs (fair prediction accuracy). We show that for an optimal classifier these three properties are in general incompatible, and we explain what common properties of data make them incompatible. Finally we provide an algorithm to verify if the trade-off between the three properties exists in a given dataset, and use the algorithm to show that this trade-off is common in real data.

Fighting Fire with Fire: Using Antidote Data to Improve Polarization and Fairness of Recommender Systems

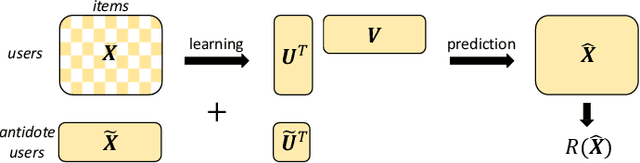
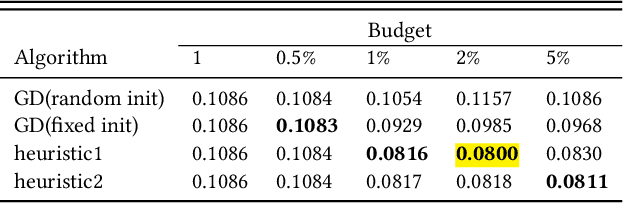
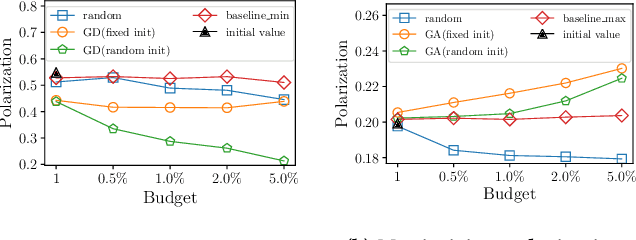
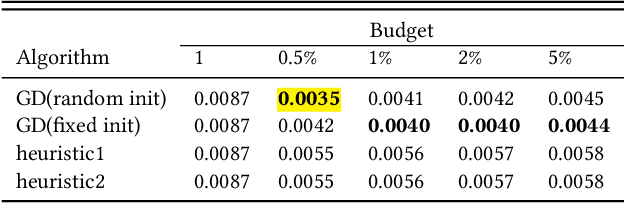
The increasing role of recommender systems in many aspects of society makes it essential to consider how such systems may impact social good. Various modifications to recommendation algorithms have been proposed to improve their performance for specific socially relevant measures. However, previous proposals are often not easily adapted to different measures, and they generally require the ability to modify either existing system inputs, the system's algorithm, or the system's outputs. As an alternative, in this paper we introduce the idea of improving the social desirability of recommender system outputs by adding more data to the input, an approach we view as as providing `antidote' data to the system. We formalize the antidote data problem, and develop optimization-based solutions. We take as our model system the matrix factorization approach to recommendation, and we propose a set of measures to capture the polarization or fairness of recommendations. We then show how to generate antidote data for each measure, pointing out a number of computational efficiencies, and discuss the impact on overall system accuracy. Our experiments show that a modest budget for antidote data can lead to significant improvements in the polarization or fairness of recommendations.

Matrix completion with queries

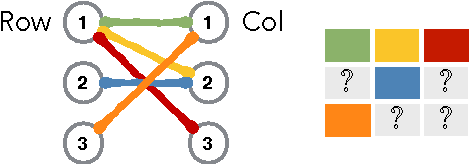
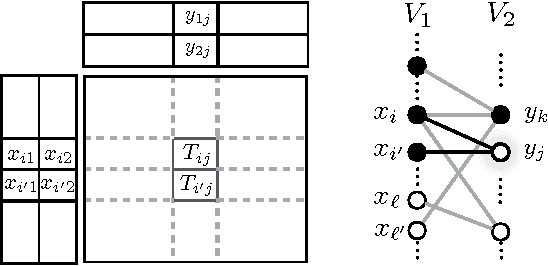
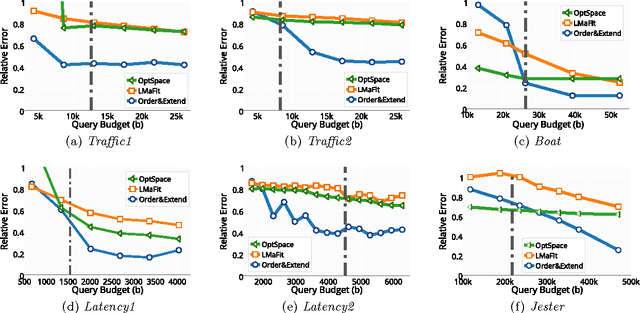
In many applications, e.g., recommender systems and traffic monitoring, the data comes in the form of a matrix that is only partially observed and low rank. A fundamental data-analysis task for these datasets is matrix completion, where the goal is to accurately infer the entries missing from the matrix. Even when the data satisfies the low-rank assumption, classical matrix-completion methods may output completions with significant error -- in that the reconstructed matrix differs significantly from the true underlying matrix. Often, this is due to the fact that the information contained in the observed entries is insufficient. In this work, we address this problem by proposing an active version of matrix completion, where queries can be made to the true underlying matrix. Subsequently, we design Order&Extend, which is the first algorithm to unify a matrix-completion approach and a querying strategy into a single algorithm. Order&Extend is able identify and alleviate insufficient information by judiciously querying a small number of additional entries. In an extensive experimental evaluation on real-world datasets, we demonstrate that our algorithm is efficient and is able to accurately reconstruct the true matrix while asking only a small number of queries.

Targeted matrix completion

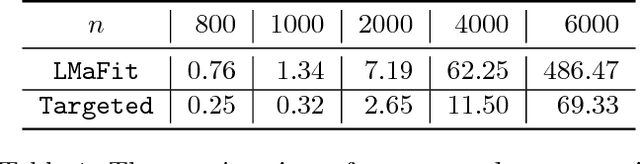
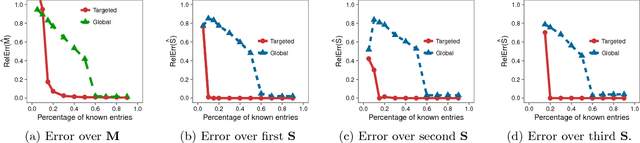
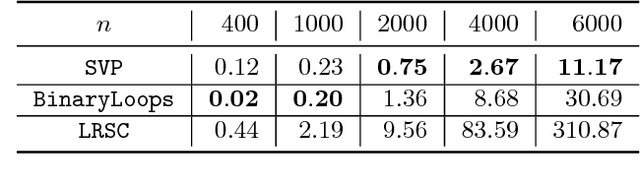
Matrix completion is a problem that arises in many data-analysis settings where the input consists of a partially-observed matrix (e.g., recommender systems, traffic matrix analysis etc.). Classical approaches to matrix completion assume that the input partially-observed matrix is low rank. The success of these methods depends on the number of observed entries and the rank of the matrix; the larger the rank, the more entries need to be observed in order to accurately complete the matrix. In this paper, we deal with matrices that are not necessarily low rank themselves, but rather they contain low-rank submatrices. We propose Targeted, which is a general framework for completing such matrices. In this framework, we first extract the low-rank submatrices and then apply a matrix-completion algorithm to these low-rank submatrices as well as the remainder matrix separately. Although for the completion itself we use state-of-the-art completion methods, our results demonstrate that Targeted achieves significantly smaller reconstruction errors than other classical matrix-completion methods. One of the key technical contributions of the paper lies in the identification of the low-rank submatrices from the input partially-observed matrices.

Multidimensional Scaling in the Poincare Disk

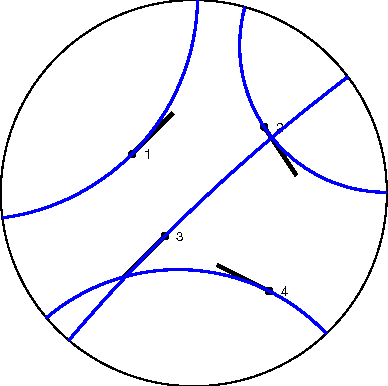
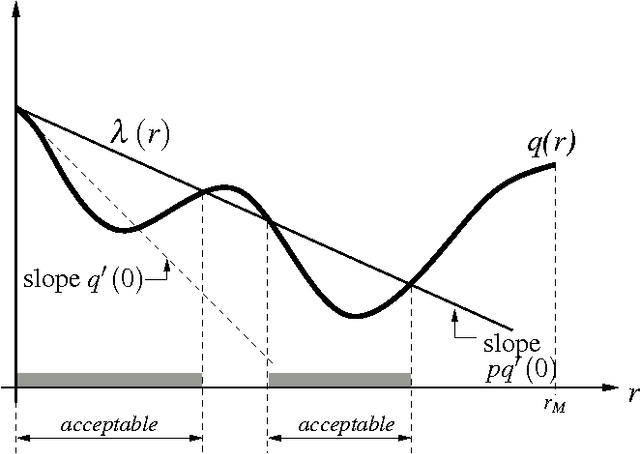
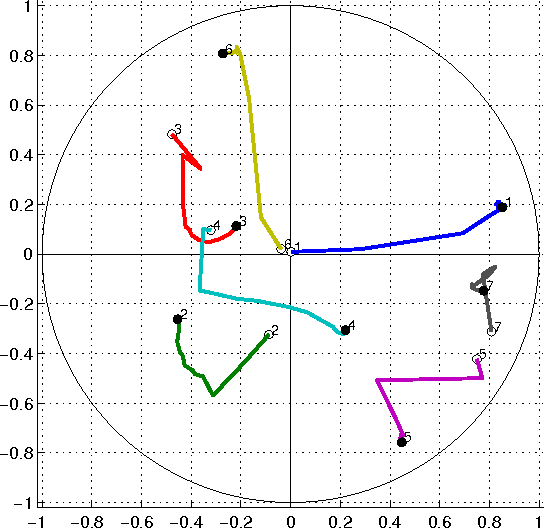
Multidimensional scaling (MDS) is a class of projective algorithms traditionally used in Euclidean space to produce two- or three-dimensional visualizations of datasets of multidimensional points or point distances. More recently however, several authors have pointed out that for certain datasets, hyperbolic target space may provide a better fit than Euclidean space. In this paper we develop PD-MDS, a metric MDS algorithm designed specifically for the Poincare disk (PD) model of the hyperbolic plane. Emphasizing the importance of proceeding from first principles in spite of the availability of various black box optimizers, our construction is based on an elementary hyperbolic line search and reveals numerous particulars that need to be carefully addressed when implementing this as well as more sophisticated iterative optimization methods in a hyperbolic space model.