Pointspectrum: Equivariance Meets Laplacian Filtering for Graph Representation Learning

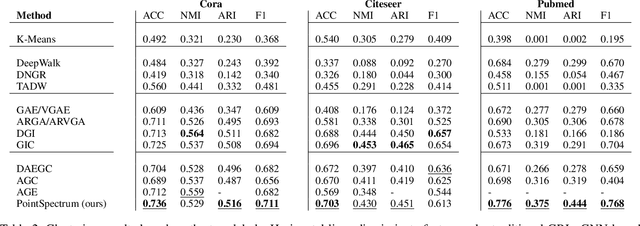
Graph Representation Learning (GRL) has become essential for modern graph data mining and learning tasks. GRL aims to capture the graph's structural information and exploit it in combination with node and edge attributes to compute low-dimensional representations. While Graph Neural Networks (GNNs) have been used in state-of-the-art GRL architectures, they have been shown to suffer from over smoothing when many GNN layers need to be stacked. In a different GRL approach, spectral methods based on graph filtering have emerged addressing over smoothing; however, up to now, they employ traditional neural networks that cannot efficiently exploit the structure of graph data. Motivated by this, we propose PointSpectrum, a spectral method that incorporates a set equivariant network to account for a graph's structure. PointSpectrum enhances the efficiency and expressiveness of spectral methods, while it outperforms or competes with state-of-the-art GRL methods. Overall, PointSpectrum addresses over smoothing by employing a graph filter and captures a graph's structure through set equivariance, lying on the intersection of GNNs and spectral methods. Our findings are promising for the benefits and applicability of this architectural shift for spectral methods and GRL.

What training reveals about neural network complexity

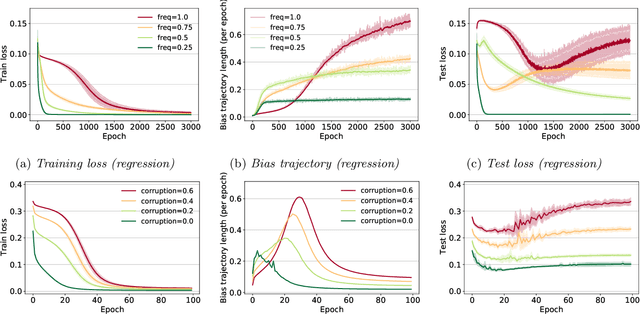
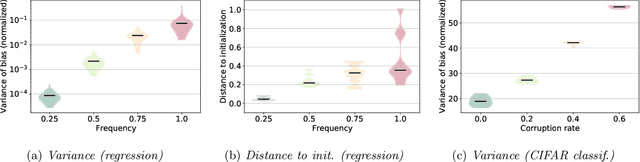
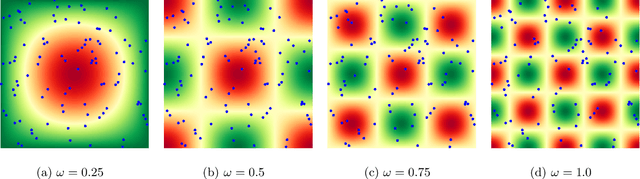
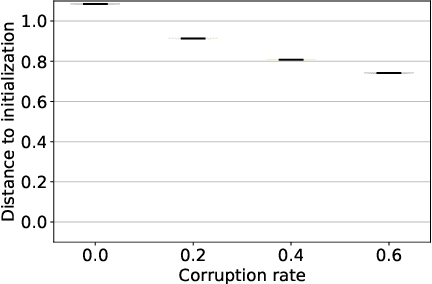
This work explores the hypothesis that the complexity of the function a deep neural network (NN) is learning can be deduced by how fast its weights change during training. Our analysis provides evidence for this supposition by relating the network's distribution of Lipschitz constants (i.e., the norm of the gradient at different regions of the input space) during different training intervals with the behavior of the stochastic training procedure. We first observe that the average Lipschitz constant close to the training data affects various aspects of the parameter trajectory, with more complex networks having a longer trajectory, bigger variance, and often veering further from their initialization. We then show that NNs whose biases are trained more steadily have bounded complexity even in regions of the input space that are far from any training point. Finally, we find that steady training with Dropout implies a training- and data-dependent generalization bound that grows poly-logarithmically with the number of parameters. Overall, our results support the hypothesis that good training behavior can be a useful bias towards good generalization.