What training reveals about neural network complexity
Paper and Code
Jun 08, 2021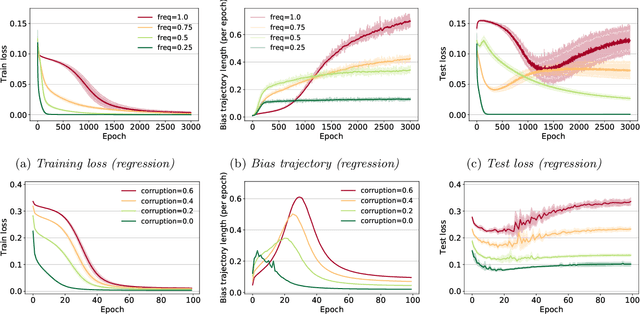
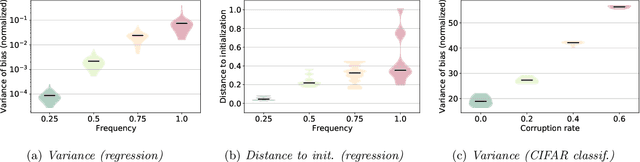
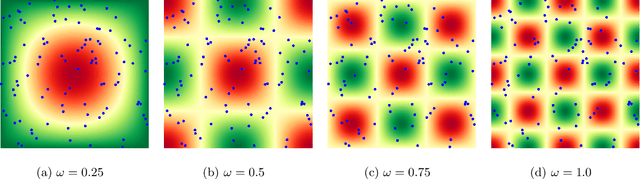
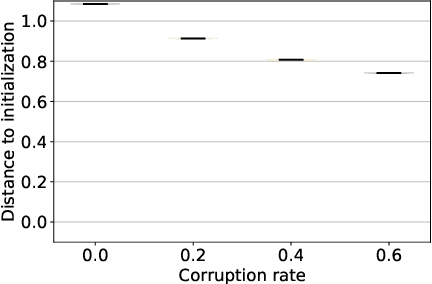
This work explores the hypothesis that the complexity of the function a deep neural network (NN) is learning can be deduced by how fast its weights change during training. Our analysis provides evidence for this supposition by relating the network's distribution of Lipschitz constants (i.e., the norm of the gradient at different regions of the input space) during different training intervals with the behavior of the stochastic training procedure. We first observe that the average Lipschitz constant close to the training data affects various aspects of the parameter trajectory, with more complex networks having a longer trajectory, bigger variance, and often veering further from their initialization. We then show that NNs whose biases are trained more steadily have bounded complexity even in regions of the input space that are far from any training point. Finally, we find that steady training with Dropout implies a training- and data-dependent generalization bound that grows poly-logarithmically with the number of parameters. Overall, our results support the hypothesis that good training behavior can be a useful bias towards good generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge