Forecasting in Non-stationary Environments with Fuzzy Time Series

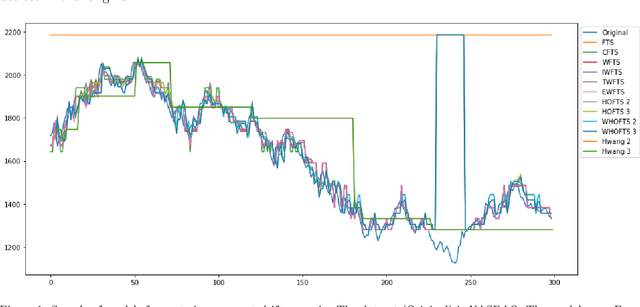
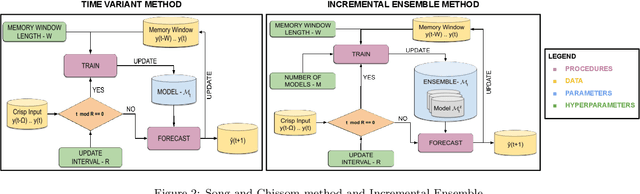
In this paper we introduce a Non-Stationary Fuzzy Time Series (NSFTS) method with time varying parameters adapted from the distribution of the data. In this approach, we employ Non-Stationary Fuzzy Sets, in which perturbation functions are used to adapt the membership function parameters in the knowledge base in response to statistical changes in the time series. The proposed method is capable of dynamically adapting its fuzzy sets to reflect the changes in the stochastic process based on the residual errors, without the need to retraining the model. This method can handle non-stationary and heteroskedastic data as well as scenarios with concept-drift. The proposed approach allows the model to be trained only once and remain useful long after while keeping reasonable accuracy. The flexibility of the method by means of computational experiments was tested with eight synthetic non-stationary time series data with several kinds of concept drifts, four real market indices (Dow Jones, NASDAQ, SP500 and TAIEX), three real FOREX pairs (EUR-USD, EUR-GBP, GBP-USD), and two real cryptocoins exchange rates (Bitcoin-USD and Ethereum-USD). As competitor models the Time Variant fuzzy time series and the Incremental Ensemble were used, these are two of the major approaches for handling non-stationary data sets. Non-parametric tests are employed to check the significance of the results. The proposed method shows resilience to concept drift, by adapting parameters of the model, while preserving the symbolic structure of the knowledge base.

Scalable and Customizable Benchmark Problems for Many-Objective Optimization

Solving many-objective problems (MaOPs) is still a significant challenge in the multi-objective optimization (MOO) field. One way to measure algorithm performance is through the use of benchmark functions (also called test functions or test suites), which are artificial problems with a well-defined mathematical formulation, known solutions and a variety of features and difficulties. In this paper we propose a parameterized generator of scalable and customizable benchmark problems for MaOPs. It is able to generate problems that reproduce features present in other benchmarks and also problems with some new features. We propose here the concept of generative benchmarking, in which one can generate an infinite number of MOO problems, by varying parameters that control specific features that the problem should have: scalability in the number of variables and objectives, bias, deceptiveness, multimodality, robust and non-robust solutions, shape of the Pareto front, and constraints. The proposed Generalized Position-Distance (GPD) tunable benchmark generator uses the position-distance paradigm, a basic approach to building test functions, used in other benchmarks such as Deb, Thiele, Laumanns and Zitzler (DTLZ), Walking Fish Group (WFG) and others. It includes scalable problems in any number of variables and objectives and it presents Pareto fronts with different characteristics. The resulting functions are easy to understand and visualize, easy to implement, fast to compute and their Pareto optimal solutions are known.