Improving Post-Earthquake Crack Detection using Semi-Synthetic Generated Images

Following an earthquake, it is vital to quickly evaluate the safety of the impacted areas. Damage detection systems, powered by computer vision and deep learning, can assist experts in this endeavor. However, the lack of extensive, labeled datasets poses a challenge to the development of these systems. In this study, we introduce a technique for generating semi-synthetic images to be used as data augmentation during the training of a damage detection system. We specifically aim to generate images of cracks, which are a prevalent and indicative form of damage. The central concept is to employ parametric meta-annotations to guide the process of generating cracks on 3D models of real-word structures. The governing parameters of these meta-annotations can be adjusted iteratively to yield images that are optimally suited for improving detectors' performance. Comparative evaluations demonstrated that a crack detection system trained with a combination of real and semi-synthetic images outperforms a system trained on real images alone.

Conditional Deep Convolutional Neural Networks for Improving the Automated Screening of Histopathological Images

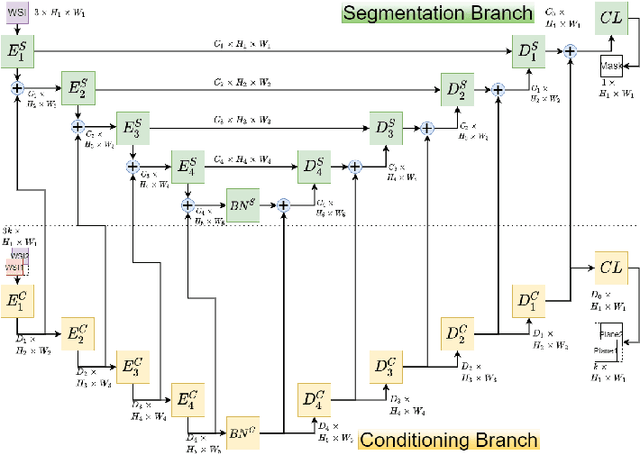
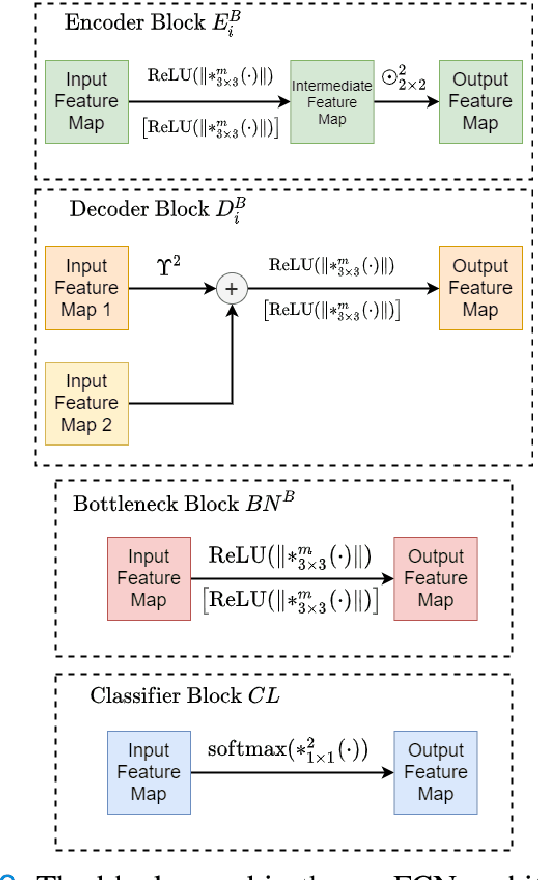
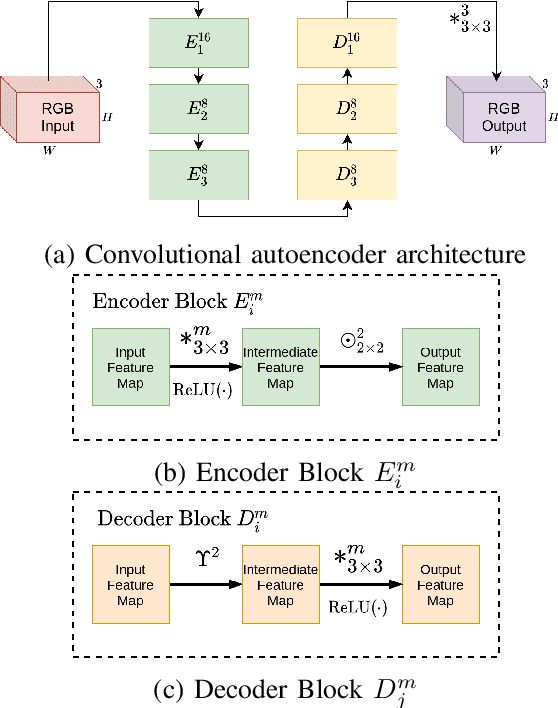
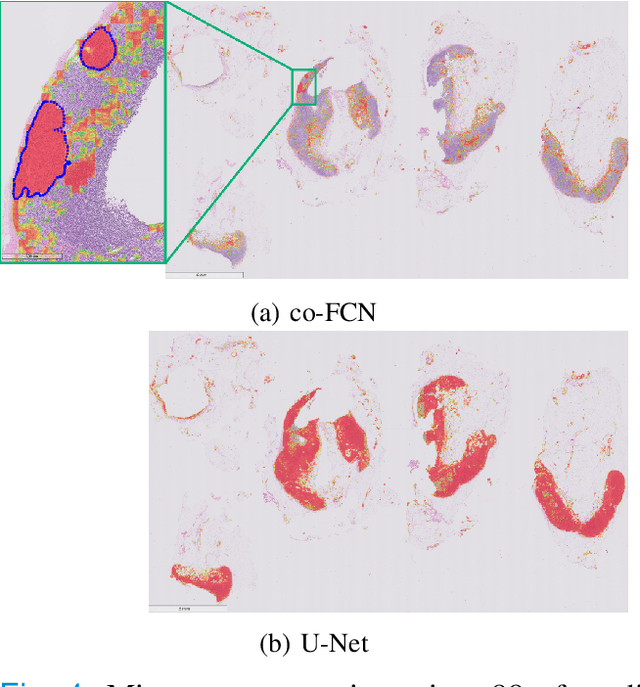
Semantic segmentation of breast cancer metastases in histopathological slides is a challenging task. In fact, significant variation in data characteristics of histopathology images (domain shift) make generalization of deep learning to unseen data difficult. Our goal is to address this challenge by using a conditional Fully Convolutional Network (co-FCN) whose output can be conditioned at run time, and which can improve its performance when a properly selected set of reference slides are used to condition the output. We adapted to our task a co-FCN originally applied to organs segmentation in volumetric medical images and we trained it on the Whole Slide Images (WSIs) from three out of five medical centers present in the CAMELYON17 dataset. We tested the performance of the network on the WSIs of the remaining centers. We also developed an automated selection strategy for selecting the conditioning subset, based on an unsupervised clustering process applied to a target-specific set of reference patches, followed by a selection policy that relies on the cluster similarities with the input patch. We benchmarked our proposed method against a U-Net trained on the same dataset with no conditioning. The conditioned network shows better performance that the U-Net on the WSIs with Isolated Tumor Cells and micro-metastases from the medical centers used as test. Our contributions are an architecture which can be applied to the histopathology domain and an automated procedure for the selection of conditioning data.

Pre-trainable Reservoir Computing with Recursive Neural Gas

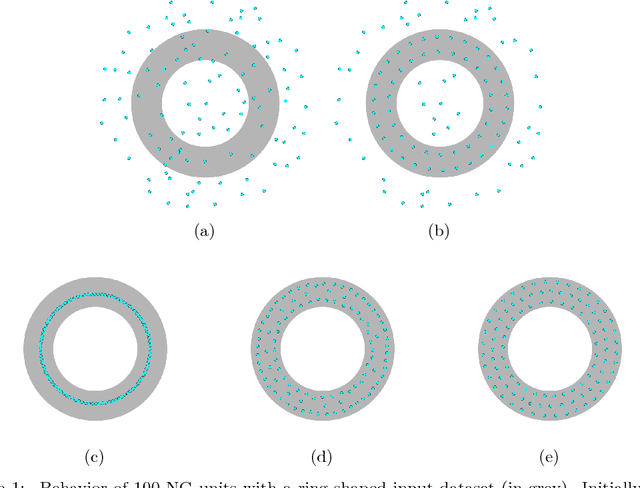
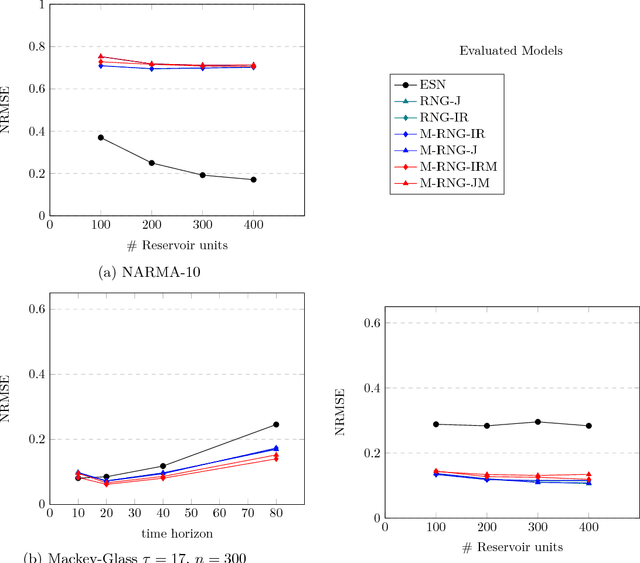
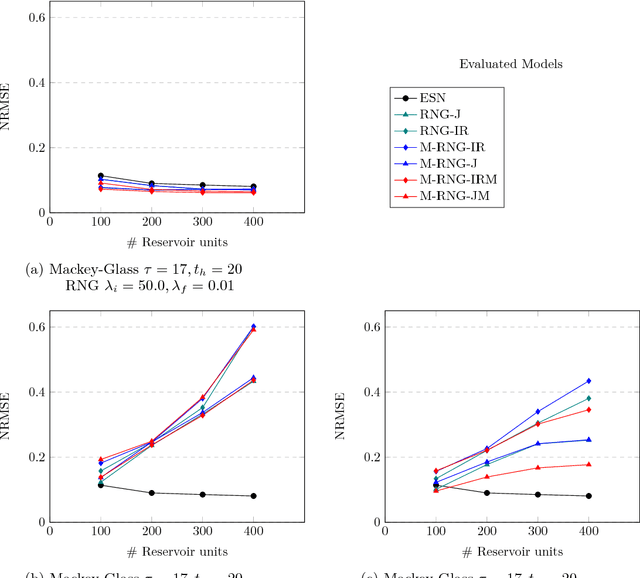
Echo State Networks (ESN) are a class of Recurrent Neural Networks (RNN) that has gained substantial popularity due to their effectiveness, ease of use and potential for compact hardware implementation. An ESN contains the three network layers input, reservoir and readout where the reservoir is the truly recurrent network. The input and reservoir layers of an ESN are initialized at random and never trained afterwards and the training of the ESN is applied to the readout layer only. The alternative of Recursive Neural Gas (RNG) is one of the many proposals of fully-trainable reservoirs that can be found in the literature. Although some improvements in performance have been reported with RNG, to the best of authors' knowledge, no experimental comparative results are known with benchmarks for which ESN is known to yield excellent results. This work describes an accurate model of RNG together with some extensions to the models presented in the literature and shows comparative results on three well-known and accepted datasets. The experimental results obtained show that, under specific circumstances, RNG-based reservoirs can achieve better performance.

Online Fall Detection using Recurrent Neural Networks

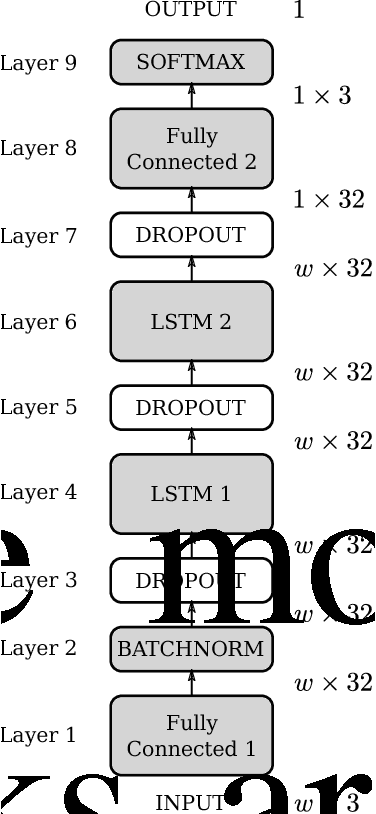
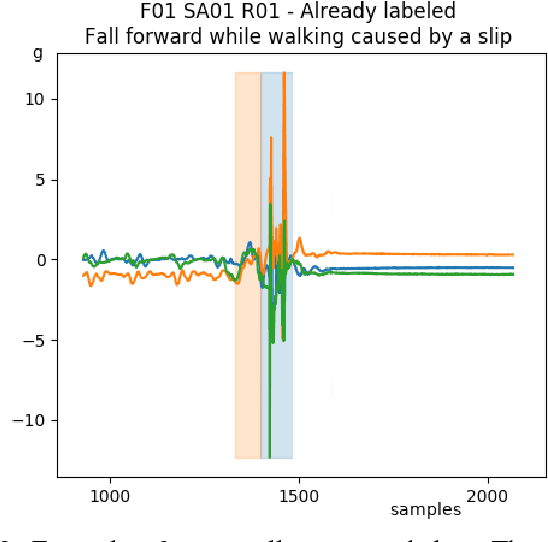
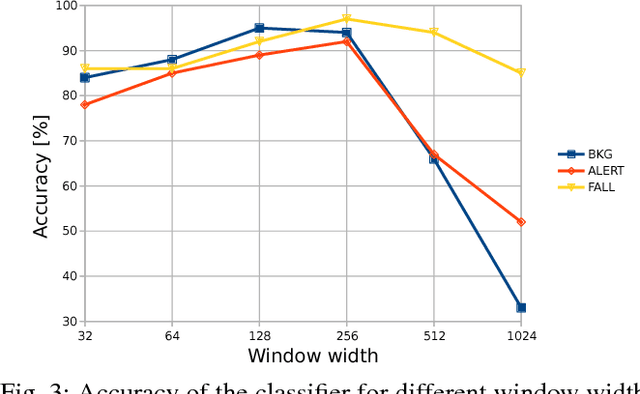
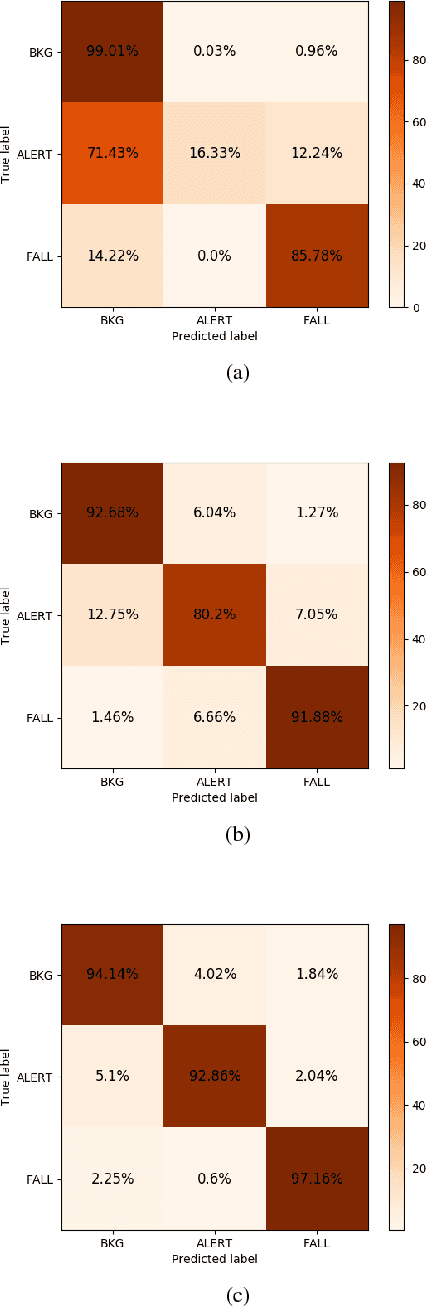
Unintentional falls can cause severe injuries and even death, especially if no immediate assistance is given. The aim of Fall Detection Systems (FDSs) is to detect an occurring fall. This information can be used to trigger the necessary assistance in case of injury. This can be done by using either ambient-based sensors, e.g. cameras, or wearable devices. The aim of this work is to study the technical aspects of FDSs based on wearable devices and artificial intelligence techniques, in particular Deep Learning (DL), to implement an effective algorithm for on-line fall detection. The proposed classifier is based on a Recurrent Neural Network (RNN) model with underlying Long Short-Term Memory (LSTM) blocks. The method is tested on the publicly available SisFall dataset, with extended annotation, and compared with the results obtained by the SisFall authors.

Some Further Evidence about Magnification and Shape in Neural Gas

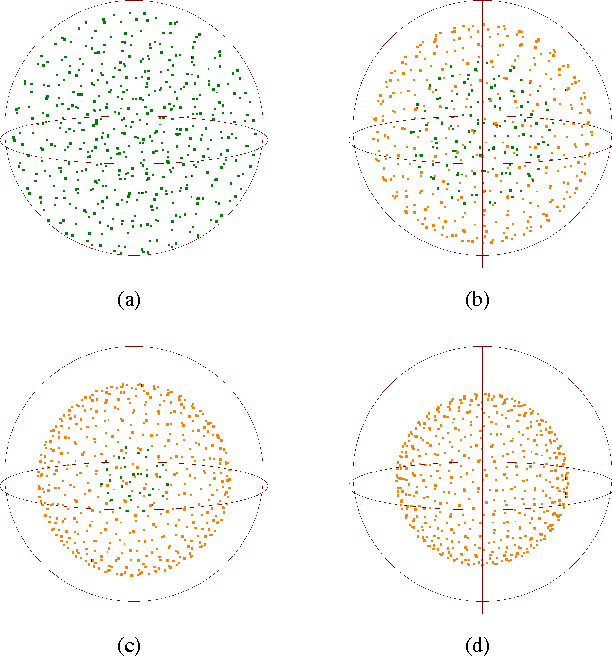
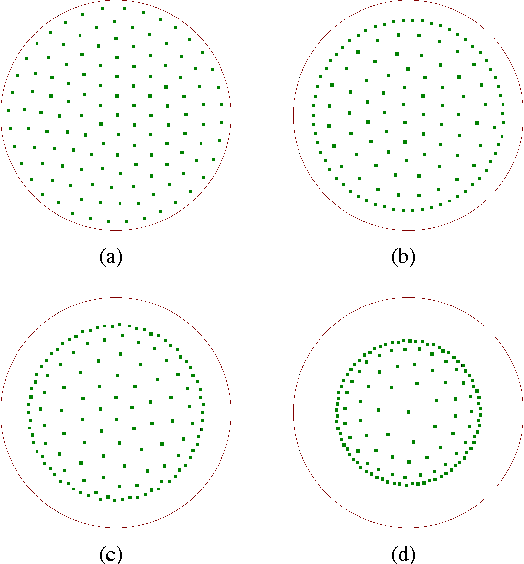
Neural gas (NG) is a robust vector quantization algorithm with a well-known mathematical model. According to this, the neural gas samples the underlying data distribution following a power law with a magnification exponent that depends on data dimensionality only. The effects of shape in the input data distribution, however, are not entirely covered by the NG model above, due to the technical difficulties involved. The experimental work described here shows that shape is indeed relevant in determining the overall NG behavior; in particular, some experiments reveal richer and complex behaviors induced by shape that cannot be explained by the power law alone. Although a more comprehensive analytical model remains to be defined, the evidence collected in these experiments suggests that the NG algorithm has an interesting potential for detecting complex shapes in noisy datasets.

A Multi-signal Variant for the GPU-based Parallelization of Growing Self-Organizing Networks

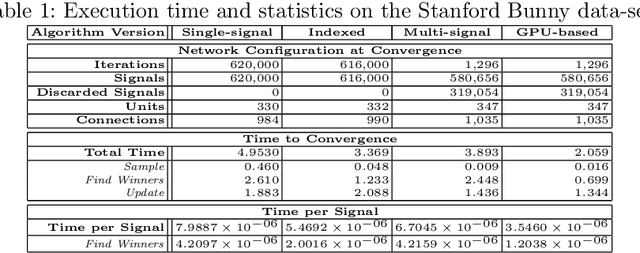
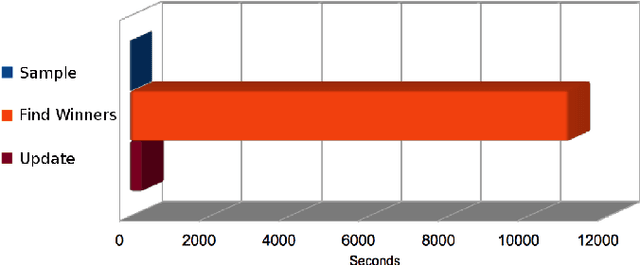
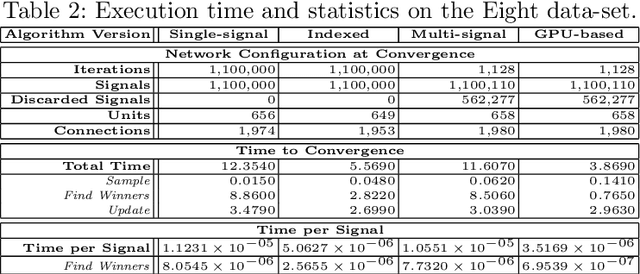
Among the many possible approaches for the parallelization of self-organizing networks, and in particular of growing self-organizing networks, perhaps the most common one is producing an optimized, parallel implementation of the standard sequential algorithms reported in the literature. In this paper we explore an alternative approach, based on a new algorithm variant specifically designed to match the features of the large-scale, fine-grained parallelism of GPUs, in which multiple input signals are processed at once. Comparative tests have been performed, using both parallel and sequential implementations of the new algorithm variant, in particular for a growing self-organizing network that reconstructs surfaces from point clouds. The experimental results show that this approach allows harnessing in a more effective way the intrinsic parallelism that the self-organizing networks algorithms seem intuitively to suggest, obtaining better performances even with networks of smaller size.

A Growing Self-Organizing Network for Reconstructing Curves and Surfaces

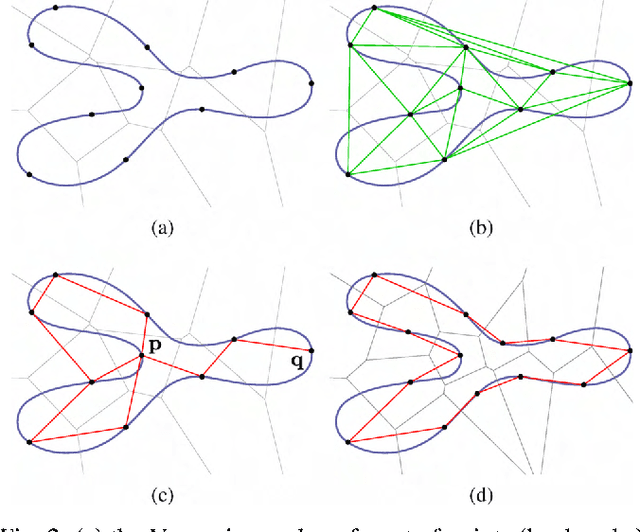
Self-organizing networks such as Neural Gas, Growing Neural Gas and many others have been adopted in actual applications for both dimensionality reduction and manifold learning. Typically, in these applications, the structure of the adapted network yields a good estimate of the topology of the unknown subspace from where the input data points are sampled. The approach presented here takes a different perspective, namely by assuming that the input space is a manifold of known dimension. In return, the new type of growing self-organizing network presented gains the ability to adapt itself in way that may guarantee the effective and stable recovery of the exact topological structure of the input manifold.