Giacomo Parigi
Some Further Evidence about Magnification and Shape in Neural Gas
Mar 28, 2015

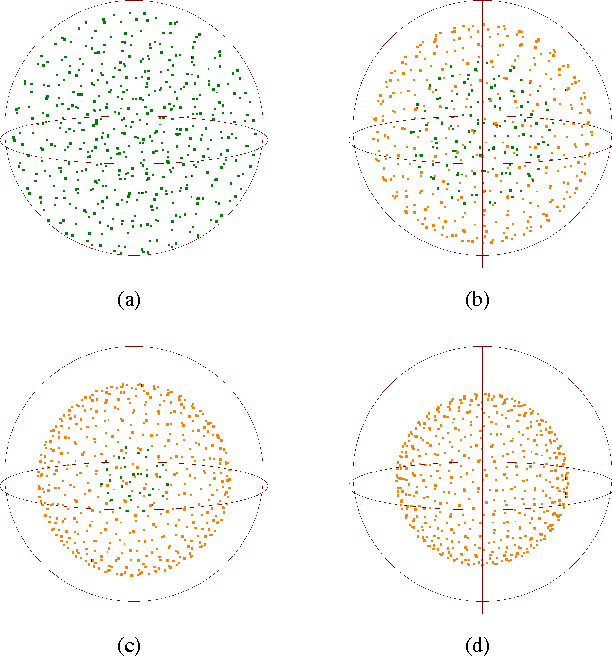
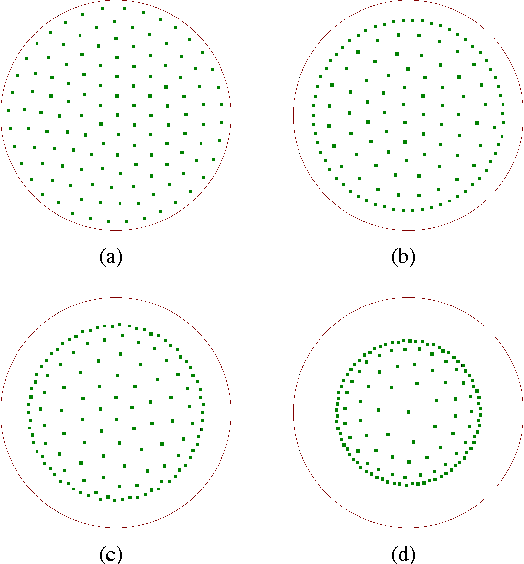
Abstract:Neural gas (NG) is a robust vector quantization algorithm with a well-known mathematical model. According to this, the neural gas samples the underlying data distribution following a power law with a magnification exponent that depends on data dimensionality only. The effects of shape in the input data distribution, however, are not entirely covered by the NG model above, due to the technical difficulties involved. The experimental work described here shows that shape is indeed relevant in determining the overall NG behavior; in particular, some experiments reveal richer and complex behaviors induced by shape that cannot be explained by the power law alone. Although a more comprehensive analytical model remains to be defined, the evidence collected in these experiments suggests that the NG algorithm has an interesting potential for detecting complex shapes in noisy datasets.
A Multi-signal Variant for the GPU-based Parallelization of Growing Self-Organizing Networks
Mar 28, 2015
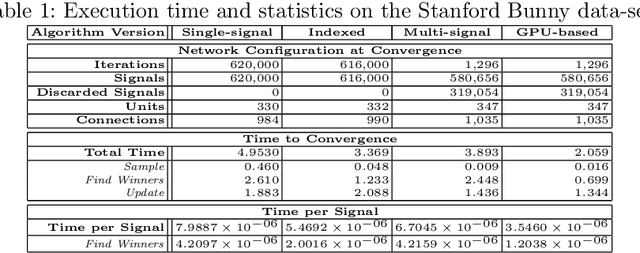
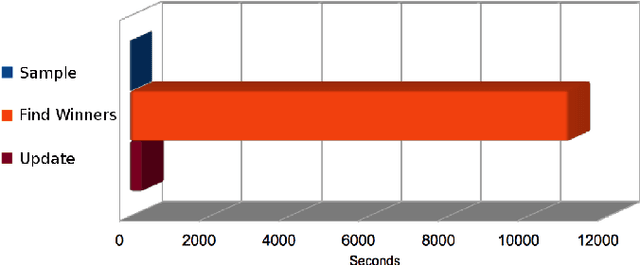
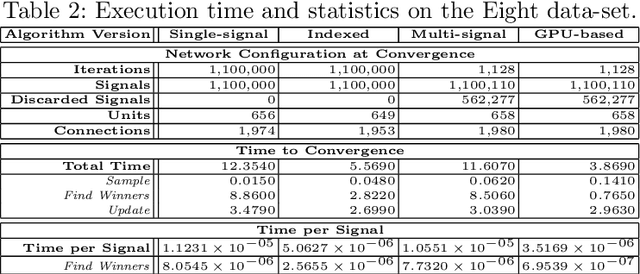
Abstract:Among the many possible approaches for the parallelization of self-organizing networks, and in particular of growing self-organizing networks, perhaps the most common one is producing an optimized, parallel implementation of the standard sequential algorithms reported in the literature. In this paper we explore an alternative approach, based on a new algorithm variant specifically designed to match the features of the large-scale, fine-grained parallelism of GPUs, in which multiple input signals are processed at once. Comparative tests have been performed, using both parallel and sequential implementations of the new algorithm variant, in particular for a growing self-organizing network that reconstructs surfaces from point clouds. The experimental results show that this approach allows harnessing in a more effective way the intrinsic parallelism that the self-organizing networks algorithms seem intuitively to suggest, obtaining better performances even with networks of smaller size.
* 17 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge