March Boedihardjo
A Performance Guarantee for Spectral Clustering
Jul 10, 2020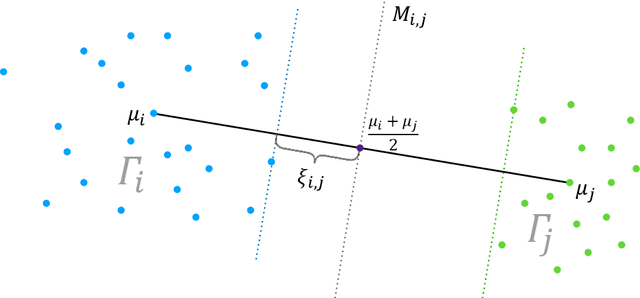
Abstract:The two-step spectral clustering method, which consists of the Laplacian eigenmap and a rounding step, is a widely used method for graph partitioning. It can be seen as a natural relaxation to the NP-hard minimum ratio cut problem. In this paper we study the central question: when is spectral clustering able to find the global solution to the minimum ratio cut problem? First we provide a condition that naturally depends on the intra- and inter-cluster connectivities of a given partition under which we may certify that this partition is the solution to the minimum ratio cut problem. Then we develop a deterministic two-to-infinity norm perturbation bound for the the invariant subspace of the graph Laplacian that corresponds to the $k$ smallest eigenvalues. Finally by combining these two results we give a condition under which spectral clustering is guaranteed to output the global solution to the minimum ratio cut problem, which serves as a performance guarantee for spectral clustering.
DP-LSSGD: A Stochastic Optimization Method to Lift the Utility in Privacy-Preserving ERM
Jun 28, 2019



Abstract:Machine learning (ML) models trained by differentially private stochastic gradient descent (DP-SGD) has much lower utility than the non-private ones. To mitigate this degradation, we propose a DP Laplacian smoothing SGD (DP-LSSGD) for privacy-preserving ML. At the core of DP-LSSGD is the Laplace smoothing operator, which smooths out the Gaussian noise vector used in the Gaussian mechanism. Under the same amount of noise used in the Gaussian mechanism, DP-LSSGD attains the same differential privacy guarantee, but a strictly better utility guarantee, excluding an intrinsic term which is usually dominated by the other terms, for convex optimization than DP-SGD by a factor which is much less than one. In practice, DP-LSSGD makes training both convex and nonconvex ML models more efficient and enables the trained models to generalize better. For ResNet20, under the same strong differential privacy guarantee, DP-LSSGD can lift the testing accuracy of the trained private model by more than $8$\% compared with DP-SGD. The proposed algorithm is simple to implement and the extra computational complexity and memory overhead compared with DP-SGD are negligible. DP-LSSGD is applicable to train a large variety of ML models, including deep neural nets. The code is available at \url{https://github.com/BaoWangMath/DP-LSSGD}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge