A Performance Guarantee for Spectral Clustering

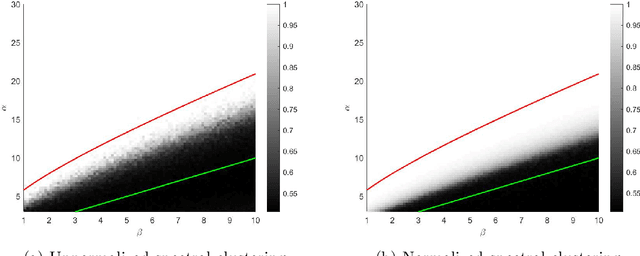
The two-step spectral clustering method, which consists of the Laplacian eigenmap and a rounding step, is a widely used method for graph partitioning. It can be seen as a natural relaxation to the NP-hard minimum ratio cut problem. In this paper we study the central question: when is spectral clustering able to find the global solution to the minimum ratio cut problem? First we provide a condition that naturally depends on the intra- and inter-cluster connectivities of a given partition under which we may certify that this partition is the solution to the minimum ratio cut problem. Then we develop a deterministic two-to-infinity norm perturbation bound for the the invariant subspace of the graph Laplacian that corresponds to the $k$ smallest eigenvalues. Finally by combining these two results we give a condition under which spectral clustering is guaranteed to output the global solution to the minimum ratio cut problem, which serves as a performance guarantee for spectral clustering.

Strong Consistency, Graph Laplacians, and the Stochastic Block Model

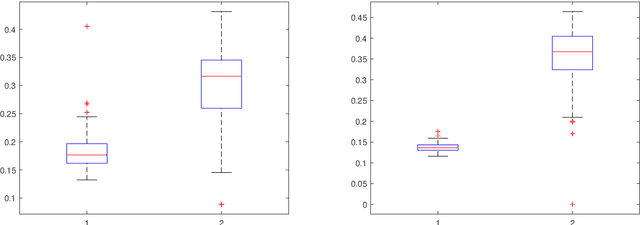
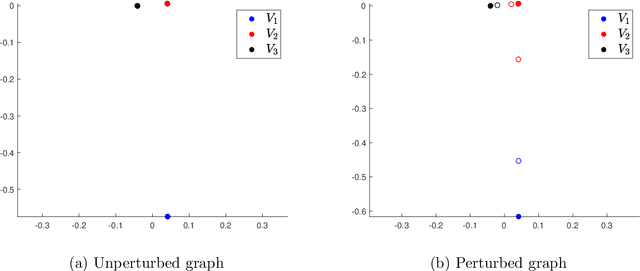
Spectral clustering has become one of the most popular algorithms in data clustering and community detection. We study the performance of classical two-step spectral clustering via the graph Laplacian to learn the stochastic block model. Our aim is to answer the following question: when is spectral clustering via the graph Laplacian able to achieve strong consistency, i.e., the exact recovery of the underlying hidden communities? Our work provides an entrywise analysis (an $\ell_{\infty}$-norm perturbation bound) of the Fielder eigenvector of both the unnormalized and the normalized Laplacian associated with the adjacency matrix sampled from the stochastic block model. We prove that spectral clustering is able to achieve exact recovery of the planted community structure under conditions that match the information-theoretic limits.