NASA Science Mission Directorate Knowledge Graph Discovery

The size of the National Aeronautics and Space Administration (NASA) Science Mission Directorate (SMD) is growing exponentially, allowing researchers to make discoveries. However, making discoveries is challenging and time-consuming due to the size of the data catalogs, and as many concepts and data are indirectly connected. This paper proposes a pipeline to generate knowledge graphs (KGs) representing different NASA SMD domains. These KGs can be used as the basis for dataset search engines, saving researchers time and supporting them in finding new connections. We collected textual data and used several modern natural language processing (NLP) methods to create the nodes and the edges of the KGs. We explore the cross-domain connections, discuss our challenges, and provide future directions to inspire researchers working on similar challenges.

Multi-layer local optima networks for the analysis of advanced local search-based algorithms

A Local Optima Network (LON) is a graph model that compresses the fitness landscape of a particular combinatorial optimization problem based on a specific neighborhood operator and a local search algorithm. Determining which and how landscape features affect the effectiveness of search algorithms is relevant for both predicting their performance and improving the design process. This paper proposes the concept of multi-layer LONs as well as a methodology to explore these models aiming at extracting metrics for fitness landscape analysis. Constructing such models, extracting and analyzing their metrics are the preliminary steps into the direction of extending the study on single neighborhood operator heuristics to more sophisticated ones that use multiple operators. Therefore, in the present paper we investigate a twolayer LON obtained from instances of a combinatorial problem using bitflip and swap operators. First, we enumerate instances of NK-landscape model and use the hill climbing heuristic to build the corresponding LONs. Then, using LON metrics, we analyze how efficiently the search might be when combining both strategies. The experiments show promising results and demonstrate the ability of multi-layer LONs to provide useful information that could be used for in metaheuristics based on multiple operators such as Variable Neighborhood Search.

Fitness Landscape Analysis of Dimensionally-Aware Genetic Programming Featuring Feynman Equations

Genetic programming is an often-used technique for symbolic regression: finding symbolic expressions that match data from an unknown function. To make the symbolic regression more efficient, one can also use dimensionally-aware genetic programming that constrains the physical units of the equation. Nevertheless, there is no formal analysis of how much dimensionality awareness helps in the regression process. In this paper, we conduct a fitness landscape analysis of dimensionallyaware genetic programming search spaces on a subset of equations from Richard Feynmans well-known lectures. We define an initialisation procedure and an accompanying set of neighbourhood operators for conducting the local search within the physical unit constraints. Our experiments show that the added information about the variable dimensionality can efficiently guide the search algorithm. Still, further analysis of the differences between the dimensionally-aware and standard genetic programming landscapes is needed to help in the design of efficient evolutionary operators to be used in a dimensionally-aware regression.

MATE: A Model-based Algorithm Tuning Engine

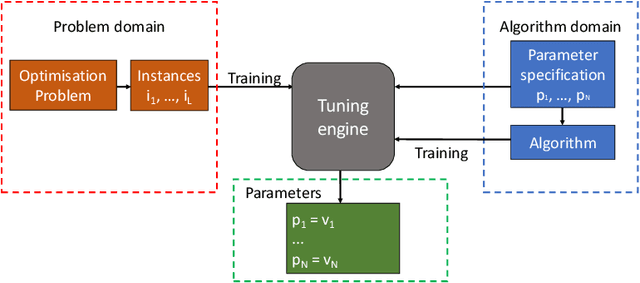
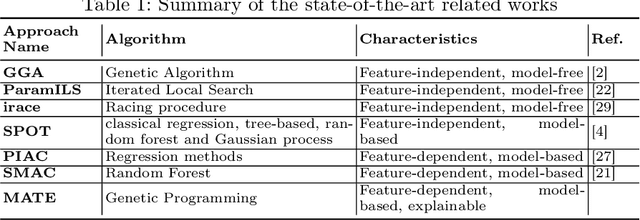
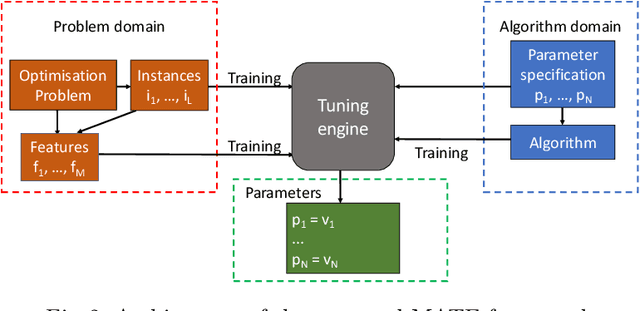
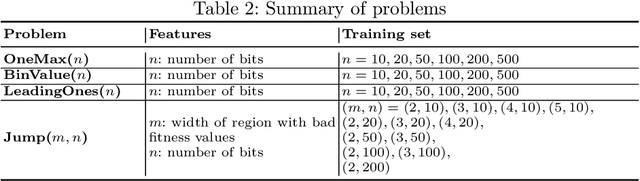
In this paper, we introduce a Model-based Algorithm Turning Engine, namely MATE, where the parameters of an algorithm are represented as expressions of the features of a target optimisation problem. In contrast to most static (feature-independent) algorithm tuning engines such as irace and SPOT, our approach aims to derive the best parameter configuration of a given algorithm for a specific problem, exploiting the relationships between the algorithm parameters and the features of the problem. We formulate the problem of finding the relationships between the parameters and the problem features as a symbolic regression problem and we use genetic programming to extract these expressions. For the evaluation, we apply our approach to configuration of the (1+1) EA and RLS algorithms for the OneMax, LeadingOnes, BinValue and Jump optimisation problems, where the theoretically optimal algorithm parameters to the problems are available as functions of the features of the problems. Our study shows that the found relationships typically comply with known theoretical results, thus demonstrating a new opportunity to consider model-based parameter tuning as an effective alternative to the static algorithm tuning engines.