On resampling vs. adjusting probabilistic graphical models in estimation of distribution algorithms

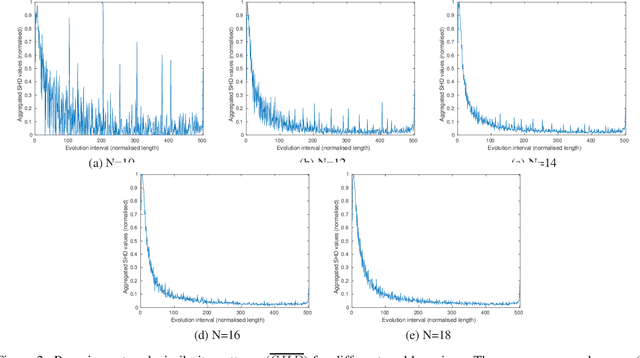
The Bayesian Optimisation Algorithm (BOA) is an Estimation of Distribution Algorithm (EDA) that uses a Bayesian network as probabilistic graphical model (PGM). Determining the optimal Bayesian network structure given a solution sample is an NP-hard problem. This step should be completed at each iteration of BOA, resulting in a very time-consuming process. For this reason most implementations use greedy estimation algorithms such as K2. However, we show in this paper that significant changes in PGM structure do not occur so frequently, and can be particularly sparse at the end of evolution. A statistical study of BOA is thus presented to characterise a pattern of PGM adjustments that can be used as a guide to reduce the frequency of PGM updates during the evolutionary process. This is accomplished by proposing a new BOA-based optimisation approach (FBOA) whose PGM is not updated at each iteration. This new approach avoids the computational burden usually found in the standard BOA. The results compare the performances of both algorithms on an NK-landscape optimisation problem using the correlation between the ruggedness and the expected runtime over enumerated instances. The experiments show that FBOA presents competitive results while significantly saving computational time.

A characterisation of S-box fitness landscapes in cryptography

Substitution Boxes (S-boxes) are nonlinear objects often used in the design of cryptographic algorithms. The design of high quality S-boxes is an interesting problem that attracts a lot of attention. Many attempts have been made in recent years to use heuristics to design S-boxes, but the results were often far from the previously known best obtained ones. Unfortunately, most of the effort went into exploring different algorithms and fitness functions while little attention has been given to the understanding why this problem is so difficult for heuristics. In this paper, we conduct a fitness landscape analysis to better understand why this problem can be difficult. Among other, we find that almost each initial starting point has its own local optimum, even though the networks are highly interconnected.

On the performance of multi-objective estimation of distribution algorithms for combinatorial problems

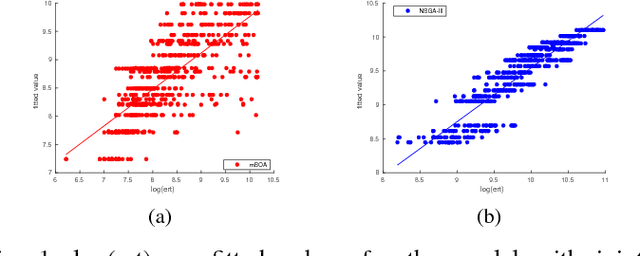
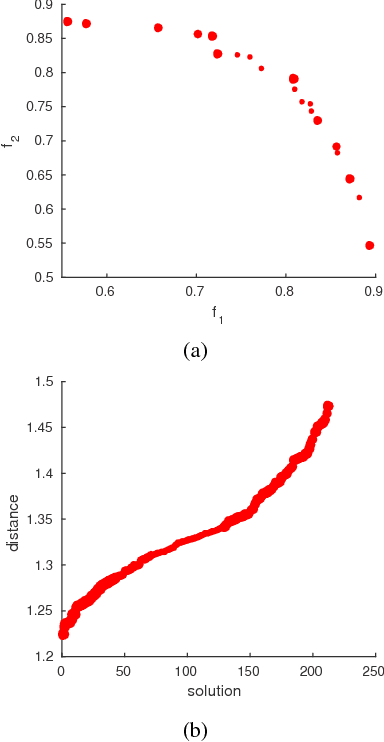
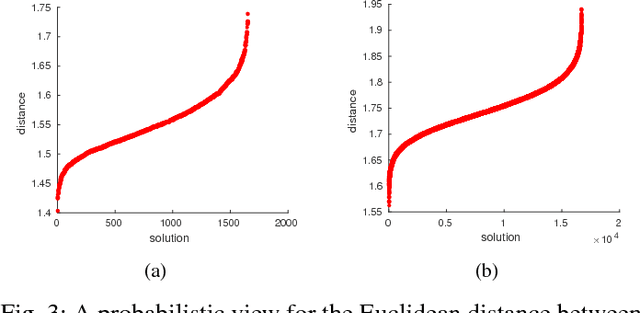
Fitness landscape analysis investigates features with a high influence on the performance of optimization algorithms, aiming to take advantage of the addressed problem characteristics. In this work, a fitness landscape analysis using problem features is performed for a Multi-objective Bayesian Optimization Algorithm (mBOA) on instances of MNK-landscape problem for 2, 3, 5 and 8 objectives. We also compare the results of mBOA with those provided by NSGA-III through the analysis of their estimated runtime necessary to identify an approximation of the Pareto front. Moreover, in order to scrutinize the probabilistic graphic model obtained by mBOA, the Pareto front is examined according to a probabilistic view. The fitness landscape study shows that mBOA is moderately or loosely influenced by some problem features, according to a simple and a multiple linear regression model, which is being proposed to predict the algorithms performance in terms of the estimated runtime. Besides, we conclude that the analysis of the probabilistic graphic model produced at the end of evolution can be useful to understand the convergence and diversity performances of the proposed approach.