Belaïd Ahiod
A Memetic Algorithm Based on Breakout Local Search for the Generalized Travelling Salesman Problem
Oct 19, 2019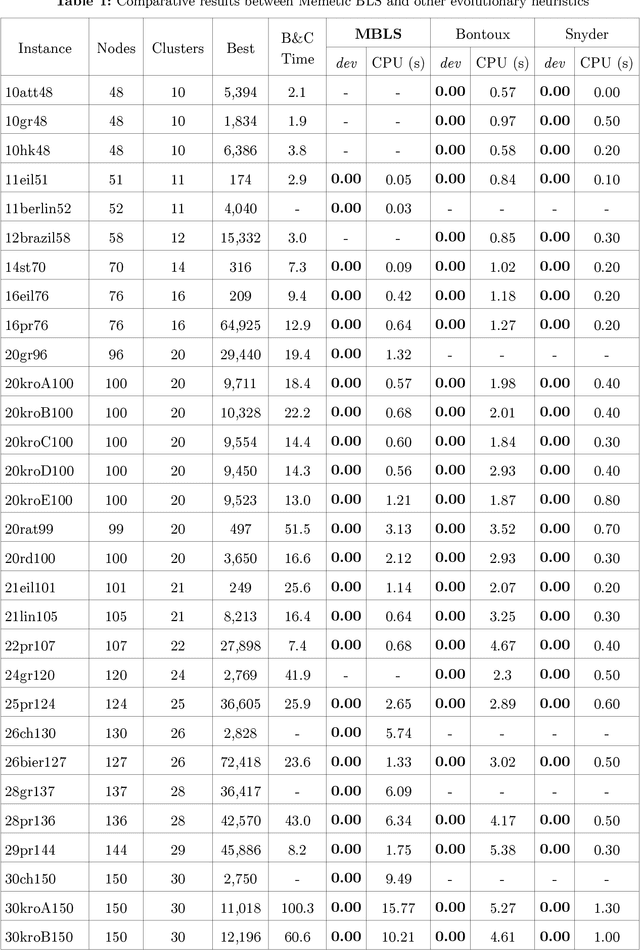
Abstract:The Travelling Salesman Problem (TSP) is one of the most popular Combinatorial Optimization Problem. It is well solicited for the large variety of applications that it can solve, but also for its difficulty to find optimal solutions. One of the variants of the TSP is the Generalized TSP (GTSP), where the TSP is considered as a special case which makes the GTSP harder to solve. We propose in this paper a new memetic algorithm based on the well-known Breakout Local Search (BLS) metaheuristic to provide good solutions for GTSP instances. Our approach is competitive compared to other recent memetic algorithms proposed for the GTSP and gives at the same time some improvements to BLS to reduce its runtime.
On the performance of multi-objective estimation of distribution algorithms for combinatorial problems
Jun 04, 2018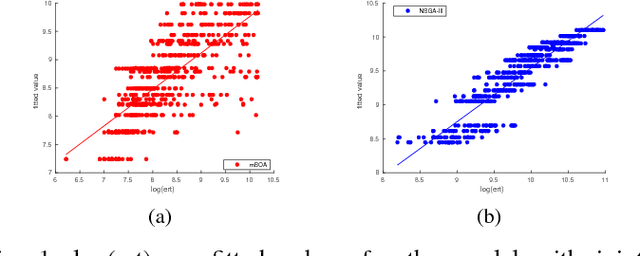
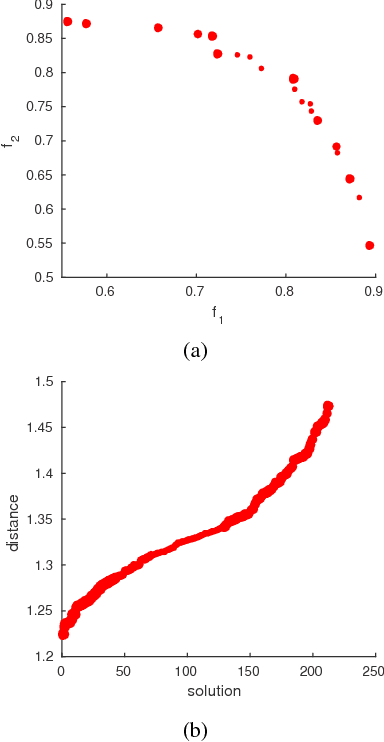
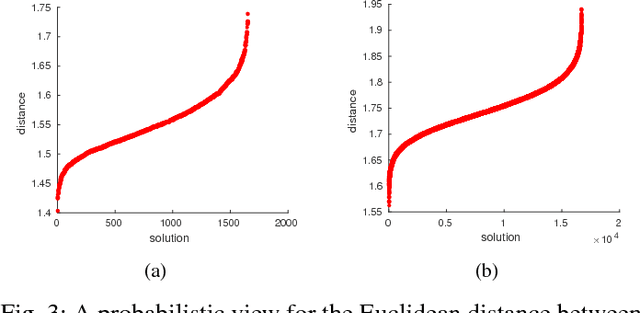

Abstract:Fitness landscape analysis investigates features with a high influence on the performance of optimization algorithms, aiming to take advantage of the addressed problem characteristics. In this work, a fitness landscape analysis using problem features is performed for a Multi-objective Bayesian Optimization Algorithm (mBOA) on instances of MNK-landscape problem for 2, 3, 5 and 8 objectives. We also compare the results of mBOA with those provided by NSGA-III through the analysis of their estimated runtime necessary to identify an approximation of the Pareto front. Moreover, in order to scrutinize the probabilistic graphic model obtained by mBOA, the Pareto front is examined according to a probabilistic view. The fitness landscape study shows that mBOA is moderately or loosely influenced by some problem features, according to a simple and a multiple linear regression model, which is being proposed to predict the algorithms performance in terms of the estimated runtime. Besides, we conclude that the analysis of the probabilistic graphic model produced at the end of evolution can be useful to understand the convergence and diversity performances of the proposed approach.
Étude de Problèmes d'Optimisation Combinatoire à Multiples Composantes Interdépendantes
Jun 22, 2016
Abstract:This extended abstract presents an overview on NP-hard optimization problems with multiple interdependent components. These problems occur in many real-world applications: industrial applications, engineering, and logistics. The fact that these problems are composed of many sub-problems that are NP-hard makes them even more challenging to solve using exact algorithms. This is mainly due to the high complexity of this class of algorithms and the hardness of the problems themselves. The main source of difficulty of these problems is the presence of internal dependencies between sub-problems. This aspect of interdependence of components is presented, and some outlines on solving approaches are briefly introduced from a (meta)heuristics and evolutionary computation perspective.
Cosolver2B: An Efficient Local Search Heuristic for the Travelling Thief Problem
Mar 23, 2016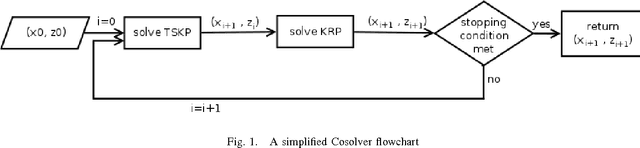
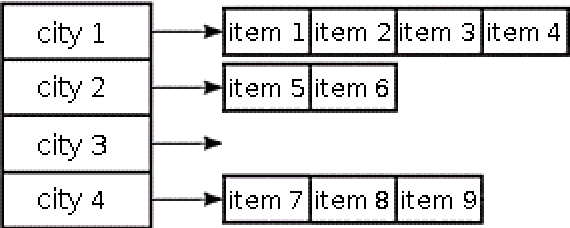
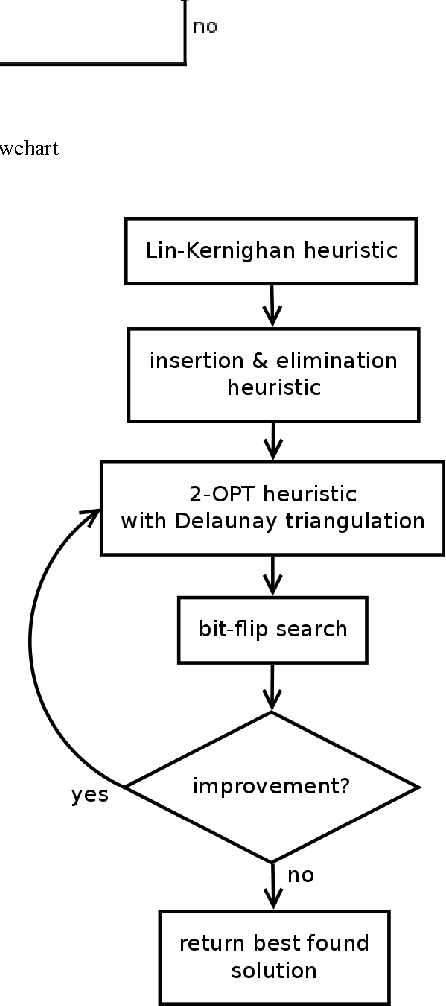
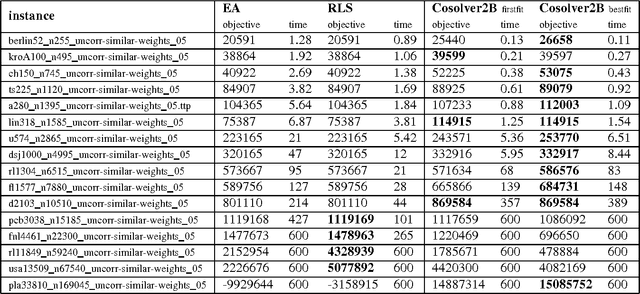
Abstract:Real-world problems are very difficult to optimize. However, many researchers have been solving benchmark problems that have been extensively investigated for the last decades even if they have very few direct applications. The Traveling Thief Problem (TTP) is a NP-hard optimization problem that aims to provide a more realistic model. TTP targets particularly routing problem under packing/loading constraints which can be found in supply chain management and transportation. In this paper, TTP is presented and formulated mathematically. A combined local search algorithm is proposed and compared with Random Local Search (RLS) and Evolutionary Algorithm (EA). The obtained results are quite promising since new better solutions were found.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge