Manvel Gasparyan
Exact Feature Collisions in Neural Networks
May 31, 2022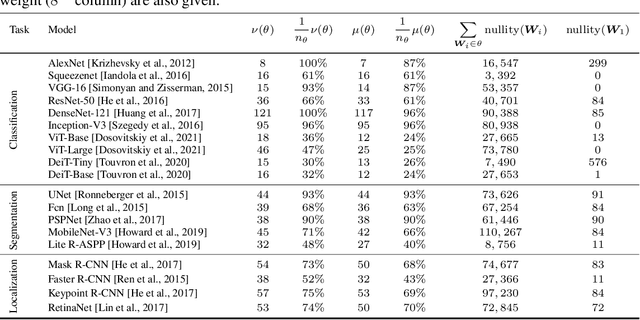
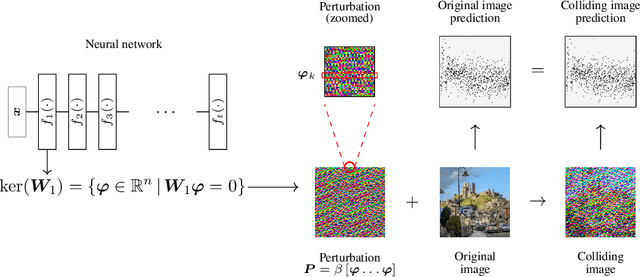

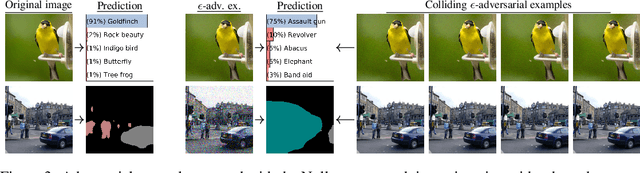
Abstract:Predictions made by deep neural networks were shown to be highly sensitive to small changes made in the input space where such maliciously crafted data points containing small perturbations are being referred to as adversarial examples. On the other hand, recent research suggests that the same networks can also be extremely insensitive to changes of large magnitude, where predictions of two largely different data points can be mapped to approximately the same output. In such cases, features of two data points are said to approximately collide, thus leading to the largely similar predictions. Our results improve and extend the work of Li et al.(2019), laying out theoretical grounds for the data points that have colluding features from the perspective of weights of neural networks, revealing that neural networks not only suffer from features that approximately collide but also suffer from features that exactly collide. We identify the necessary conditions for the existence of such scenarios, hereby investigating a large number of DNNs that have been used to solve various computer vision problems. Furthermore, we propose the Null-space search, a numerical approach that does not rely on heuristics, to create data points with colliding features for any input and for any task, including, but not limited to, classification, localization, and segmentation.
Perturbation Analysis of Gradient-based Adversarial Attacks
Jun 02, 2020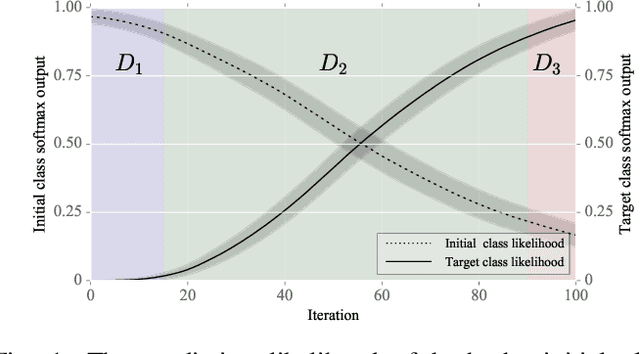
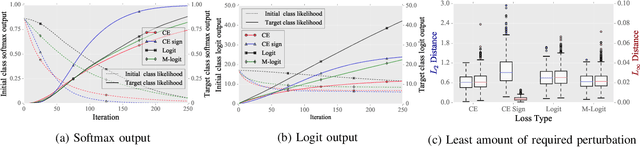
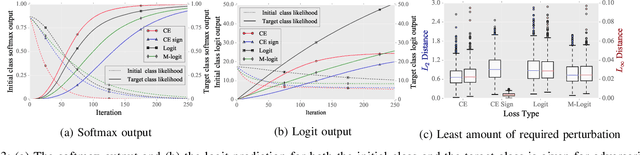
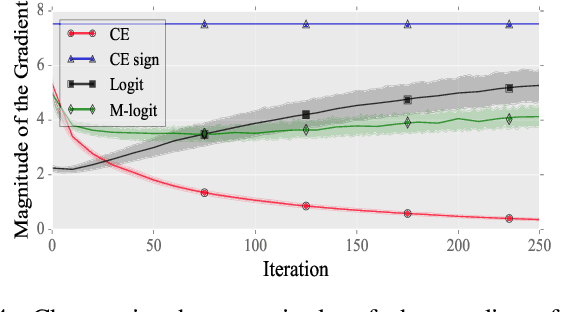
Abstract:After the discovery of adversarial examples and their adverse effects on deep learning models, many studies focused on finding more diverse methods to generate these carefully crafted samples. Although empirical results on the effectiveness of adversarial example generation methods against defense mechanisms are discussed in detail in the literature, an in-depth study of the theoretical properties and the perturbation effectiveness of these adversarial attacks has largely been lacking. In this paper, we investigate the objective functions of three popular methods for adversarial example generation: the L-BFGS attack, the Iterative Fast Gradient Sign attack, and Carlini & Wagner's attack (CW). Specifically, we perform a comparative and formal analysis of the loss functions underlying the aforementioned attacks while laying out large-scale experimental results on ImageNet dataset. This analysis exposes (1) the faster optimization speed as well as the constrained optimization space of the cross-entropy loss, (2) the detrimental effects of using the signature of the cross-entropy loss on optimization precision as well as optimization space, and (3) the slow optimization speed of the logit loss in the context of adversariality. Our experiments reveal that the Iterative Fast Gradient Sign attack, which is thought to be fast for generating adversarial examples, is the worst attack in terms of the number of iterations required to create adversarial examples in the setting of equal perturbation. Moreover, our experiments show that the underlying loss function of CW, which is criticized for being substantially slower than other adversarial attacks, is not that much slower than other loss functions. Finally, we analyze how well neural networks can identify adversarial perturbations generated by the attacks under consideration, hereby revisiting the idea of adversarial retraining on ImageNet.
* Accepted for publication in Pattern Recognition Letters, 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge