Mansooreh Mollaghasemi
Multi-Task Learning Using Neighborhood Kernels
Jul 11, 2017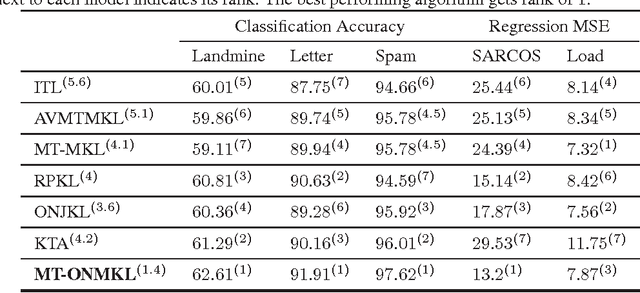
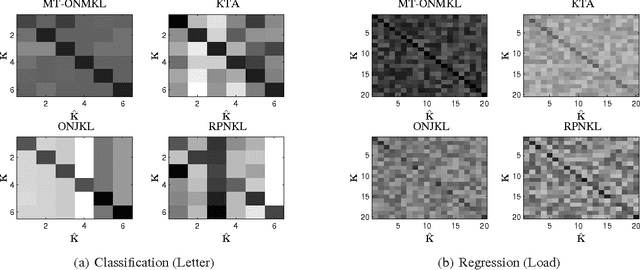
Abstract:This paper introduces a new and effective algorithm for learning kernels in a Multi-Task Learning (MTL) setting. Although, we consider a MTL scenario here, our approach can be easily applied to standard single task learning, as well. As shown by our empirical results, our algorithm consistently outperforms the traditional kernel learning algorithms such as uniform combination solution, convex combinations of base kernels as well as some kernel alignment-based models, which have been proven to give promising results in the past. We present a Rademacher complexity bound based on which a new Multi-Task Multiple Kernel Learning (MT-MKL) model is derived. In particular, we propose a Support Vector Machine-regularized model in which, for each task, an optimal kernel is learned based on a neighborhood-defining kernel that is not restricted to be positive semi-definite. Comparative experimental results are showcased that underline the merits of our neighborhood-defining framework in both classification and regression problems.
Local Rademacher Complexity-based Learning Guarantees for Multi-Task Learning
Feb 09, 2017Abstract:We show a Talagrand-type concentration inequality for Multi-Task Learning (MTL), using which we establish sharp excess risk bounds for MTL in terms of distribution- and data-dependent versions of the Local Rademacher Complexity (LRC). We also give a new bound on the LRC for norm regularized as well as strongly convex hypothesis classes, which applies not only to MTL but also to the standard i.i.d. setting. Combining both results, one can now easily derive fast-rate bounds on the excess risk for many prominent MTL methods, including---as we demonstrate---Schatten-norm, group-norm, and graph-regularized MTL. The derived bounds reflect a relationship akeen to a conservation law of asymptotic convergence rates. This very relationship allows for trading off slower rates w.r.t. the number of tasks for faster rates with respect to the number of available samples per task, when compared to the rates obtained via a traditional, global Rademacher analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge