Multi-Task Learning Using Neighborhood Kernels

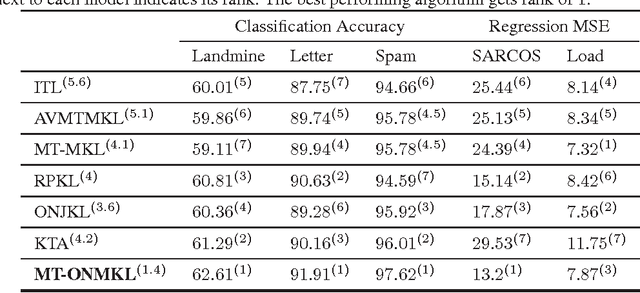
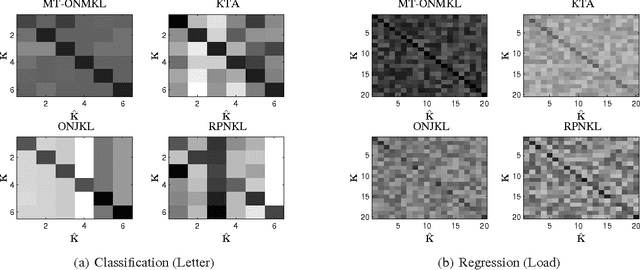
This paper introduces a new and effective algorithm for learning kernels in a Multi-Task Learning (MTL) setting. Although, we consider a MTL scenario here, our approach can be easily applied to standard single task learning, as well. As shown by our empirical results, our algorithm consistently outperforms the traditional kernel learning algorithms such as uniform combination solution, convex combinations of base kernels as well as some kernel alignment-based models, which have been proven to give promising results in the past. We present a Rademacher complexity bound based on which a new Multi-Task Multiple Kernel Learning (MT-MKL) model is derived. In particular, we propose a Support Vector Machine-regularized model in which, for each task, an optimal kernel is learned based on a neighborhood-defining kernel that is not restricted to be positive semi-definite. Comparative experimental results are showcased that underline the merits of our neighborhood-defining framework in both classification and regression problems.