TenAd: A Tensor-based Low-rank Black Box Adversarial Attack for Video Classification

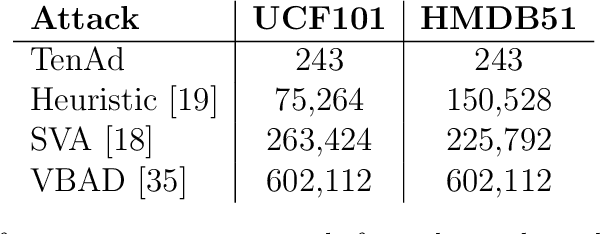
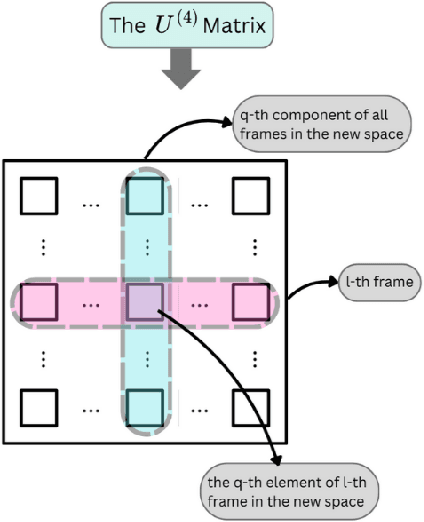
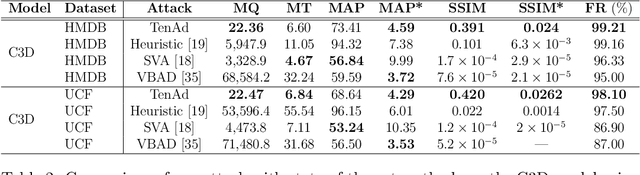
Deep learning models have achieved remarkable success in computer vision but remain vulnerable to adversarial attacks, particularly in black-box settings where model details are unknown. Existing adversarial attack methods(even those works with key frames) often treat video data as simple vectors, ignoring their inherent multi-dimensional structure, and require a large number of queries, making them inefficient and detectable. In this paper, we propose \textbf{TenAd}, a novel tensor-based low-rank adversarial attack that leverages the multi-dimensional properties of video data by representing videos as fourth-order tensors. By exploiting low-rank attack, our method significantly reduces the search space and the number of queries needed to generate adversarial examples in black-box settings. Experimental results on standard video classification datasets demonstrate that \textbf{TenAd} effectively generates imperceptible adversarial perturbations while achieving higher attack success rates and query efficiency compared to state-of-the-art methods. Our approach outperforms existing black-box adversarial attacks in terms of success rate, query efficiency, and perturbation imperceptibility, highlighting the potential of tensor-based methods for adversarial attacks on video models.

Heterogeneous Multi-Agent Reinforcement Learning via Mirror Descent Policy Optimization

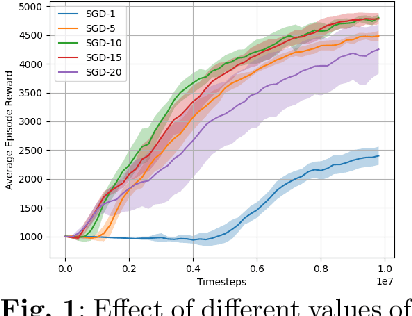
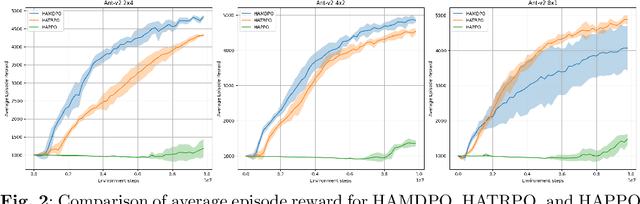
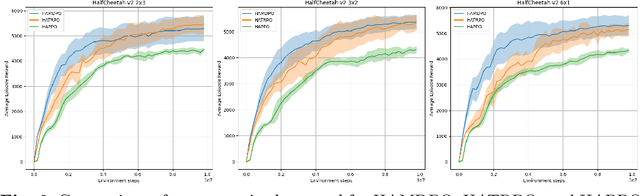
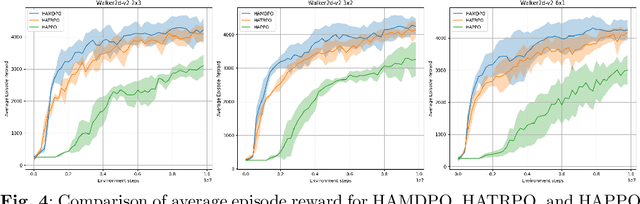
This paper presents an extension of the Mirror Descent method to overcome challenges in cooperative Multi-Agent Reinforcement Learning (MARL) settings, where agents have varying abilities and individual policies. The proposed Heterogeneous-Agent Mirror Descent Policy Optimization (HAMDPO) algorithm utilizes the multi-agent advantage decomposition lemma to enable efficient policy updates for each agent while ensuring overall performance improvements. By iteratively updating agent policies through an approximate solution of the trust-region problem, HAMDPO guarantees stability and improves performance. Moreover, the HAMDPO algorithm is capable of handling both continuous and discrete action spaces for heterogeneous agents in various MARL problems. We evaluate HAMDPO on Multi-Agent MuJoCo and StarCraftII tasks, demonstrating its superiority over state-of-the-art algorithms such as HATRPO and HAPPO. These results suggest that HAMDPO is a promising approach for solving cooperative MARL problems and could potentially be extended to address other challenging problems in the field of MARL.

Multidimensional Data Analysis Based on Block Convolutional Tensor Decomposition

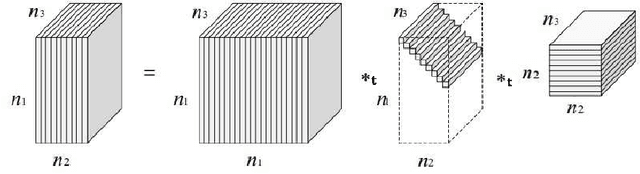
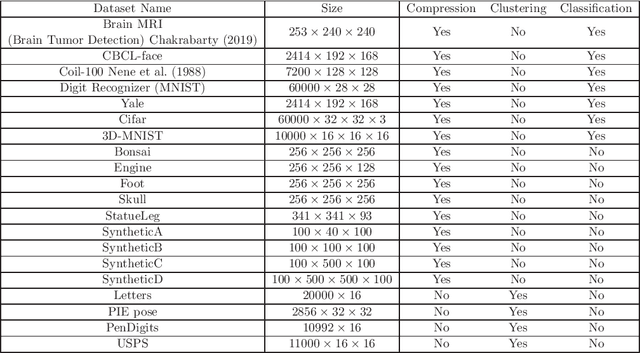
Tensor decompositions are powerful tools for analyzing multi-dimensional data in their original format. Besides tensor decompositions like Tucker and CP, Tensor SVD (t-SVD) which is based on the t-product of tensors is another extension of SVD to tensors that recently developed and has found numerous applications in analyzing high dimensional data. This paper offers a new insight into the t-Product and shows that this product is a block convolution of two tensors with periodic boundary conditions. Based on this viewpoint, we propose a new tensor-tensor product called the $\star_c{}\text{-Product}$ based on Block convolution with reflective boundary conditions. Using a tensor framework, this product can be easily extended to tensors of arbitrary order. Additionally, we introduce a tensor decomposition based on our $\star_c{}\text{-Product}$ for arbitrary order tensors. Compared to t-SVD, our new decomposition has lower complexity, and experiments show that it yields higher-quality results in applications such as classification and compression.

Local and Global Structure Preservation Based Spectral Clustering

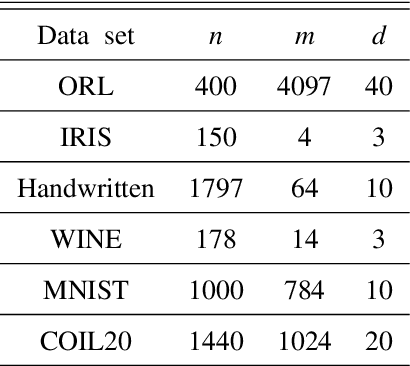
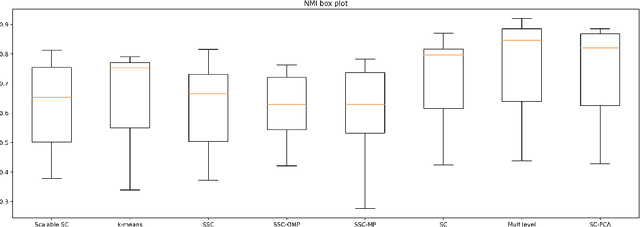
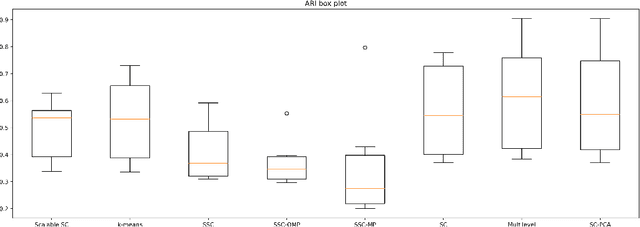
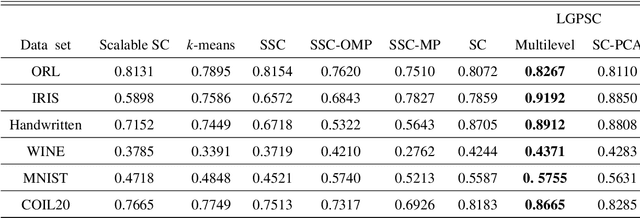
Spectral Clustering (SC) is widely used for clustering data on a nonlinear manifold. SC aims to cluster data by considering the preservation of the local neighborhood structure on the manifold data. This paper extends Spectral Clustering to Local and Global Structure Preservation Based Spectral Clustering (LGPSC) that incorporates both global structure and local neighborhood structure simultaneously. For this extension, LGPSC proposes two models to extend local structures preservation to local and global structures preservation: Spectral clustering guided Principal component analysis model and Multilevel model. Finally, we compare the experimental results of the state-of-the-art methods with our two models of LGPSC on various data sets such that the experimental results confirm the effectiveness of our LGPSC models to cluster nonlinear data.

An adaptive synchronization approach for weights of deep reinforcement learning

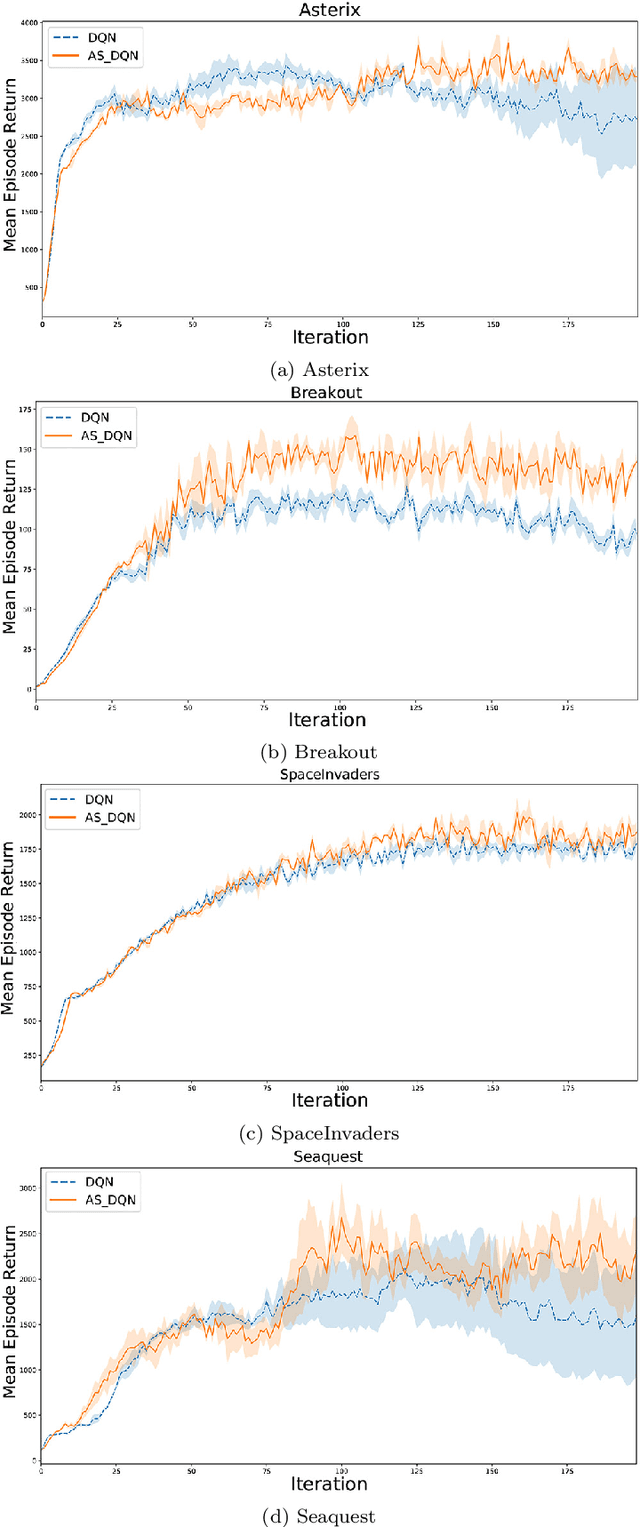
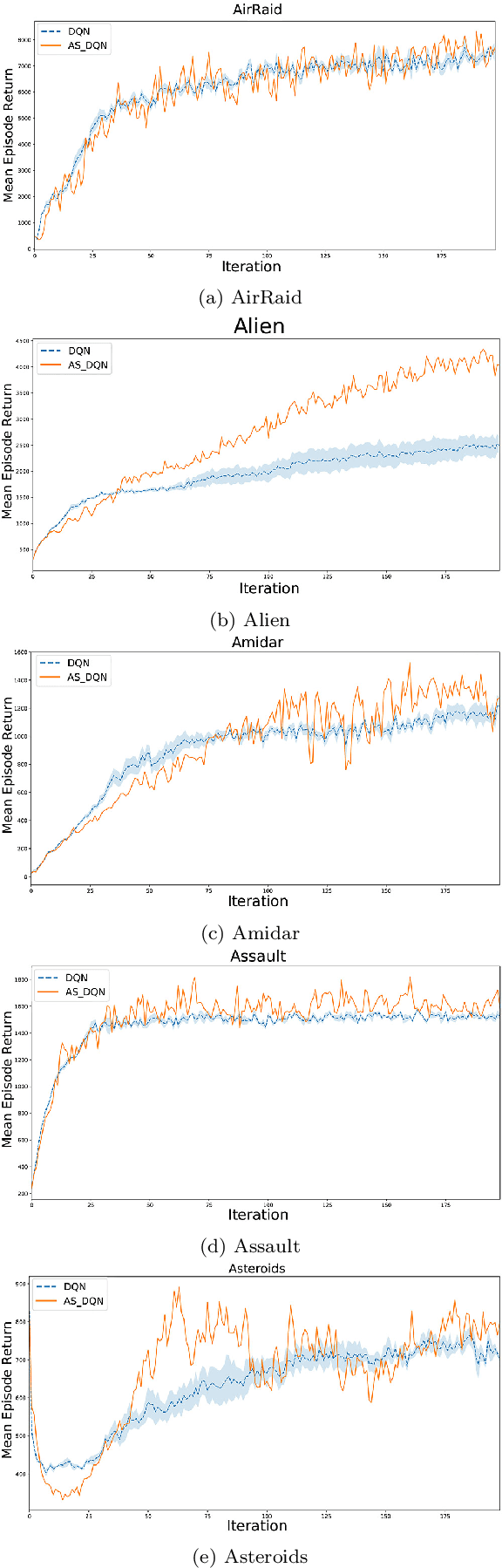
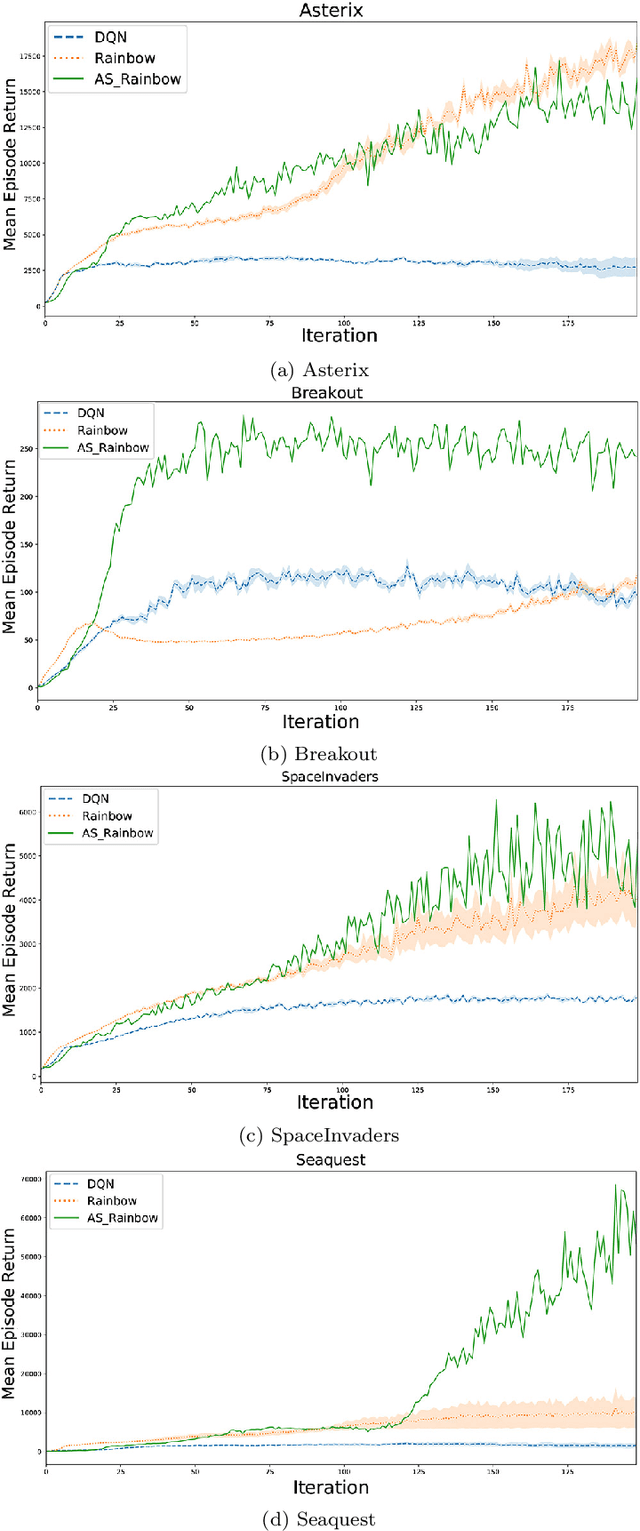
Deep Q-Networks (DQN) is one of the most well-known methods of deep reinforcement learning, which uses deep learning to approximate the action-value function. Solving numerous Deep reinforcement learning challenges such as moving targets problem and the correlation between samples are the main advantages of this model. Although there have been various extensions of DQN in recent years, they all use a similar method to DQN to overcome the problem of moving targets. Despite the advantages mentioned, synchronizing the network weight in a fixed step size, independent of the agent's behavior, may in some cases cause the loss of some properly learned networks. These lost networks may lead to states with more rewards, hence better samples stored in the replay memory for future training. In this paper, we address this problem from the DQN family and provide an adaptive approach for the synchronization of the neural weights used in DQN. In this method, the synchronization of weights is done based on the recent behavior of the agent, which is measured by a criterion at the end of the intervals. To test this method, we adjusted the DQN and rainbow methods with the proposed adaptive synchronization method. We compared these adjusted methods with their standard form on well-known games, which results confirm the quality of our synchronization methods.

A novel extension of Generalized Low-Rank Approximation of Matrices based on multiple-pairs of transformations

Dimension reduction is a main step in learning process which plays a essential role in many applications. The most popular methods in this field like SVD, PCA, and LDA, only can apply to vector data. This means that for higher order data like matrices or more generally tensors, data should be fold to a vector. By this folding, the probability of overfitting is increased and also maybe some important spatial features are ignored. Then, to tackle these issues, methods are proposed which work directly on data with their own format like GLRAM, MPCA, and MLDA. In these methods the spatial relationship among data are preserved and furthermore, the probability of overfitiing has fallen. Also the time and space complexity are less than vector-based ones. Having said that, because of the less parameters in multilinear methods, they have a much smaller search space to find an optimal answer in comparison with vector-based approach. To overcome this drawback of multilinear methods like GLRAM, we proposed a new method which is a general form of GLRAM and by preserving the merits of it have a larger search space. We have done plenty of experiments to show that our proposed method works better than GLRAM. Also, applying this approach to other multilinear dimension reduction methods like MPCA and MLDA is straightforwar