Local and Global Structure Preservation Based Spectral Clustering

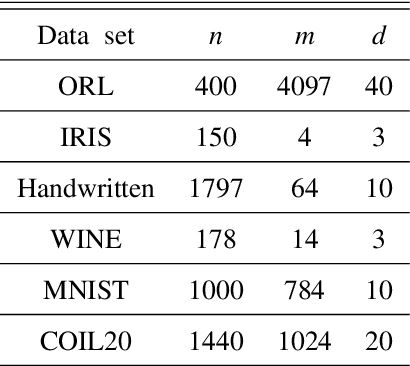
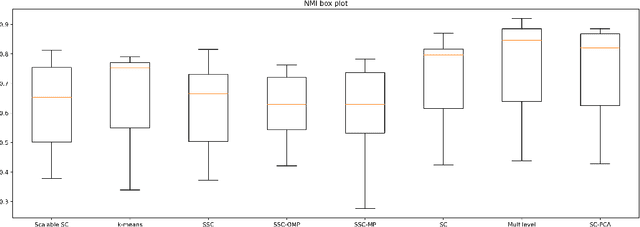
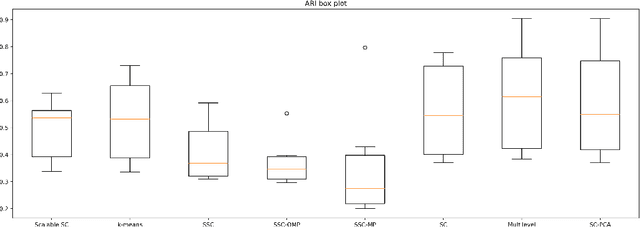
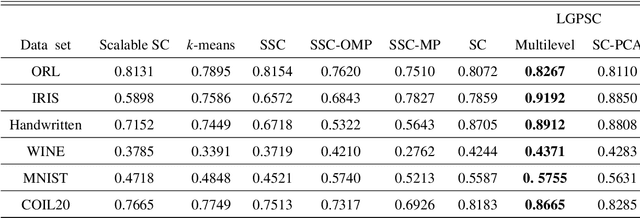
Spectral Clustering (SC) is widely used for clustering data on a nonlinear manifold. SC aims to cluster data by considering the preservation of the local neighborhood structure on the manifold data. This paper extends Spectral Clustering to Local and Global Structure Preservation Based Spectral Clustering (LGPSC) that incorporates both global structure and local neighborhood structure simultaneously. For this extension, LGPSC proposes two models to extend local structures preservation to local and global structures preservation: Spectral clustering guided Principal component analysis model and Multilevel model. Finally, we compare the experimental results of the state-of-the-art methods with our two models of LGPSC on various data sets such that the experimental results confirm the effectiveness of our LGPSC models to cluster nonlinear data.