Mahdi Molavi
Multidimensional Data Analysis Based on Block Convolutional Tensor Decomposition
Aug 11, 2023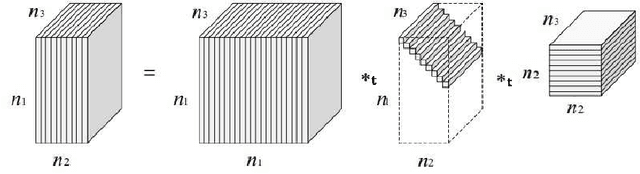
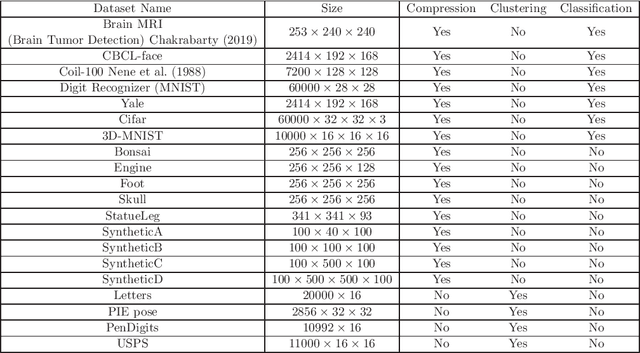


Abstract:Tensor decompositions are powerful tools for analyzing multi-dimensional data in their original format. Besides tensor decompositions like Tucker and CP, Tensor SVD (t-SVD) which is based on the t-product of tensors is another extension of SVD to tensors that recently developed and has found numerous applications in analyzing high dimensional data. This paper offers a new insight into the t-Product and shows that this product is a block convolution of two tensors with periodic boundary conditions. Based on this viewpoint, we propose a new tensor-tensor product called the $\star_c{}\text{-Product}$ based on Block convolution with reflective boundary conditions. Using a tensor framework, this product can be easily extended to tensors of arbitrary order. Additionally, we introduce a tensor decomposition based on our $\star_c{}\text{-Product}$ for arbitrary order tensors. Compared to t-SVD, our new decomposition has lower complexity, and experiments show that it yields higher-quality results in applications such as classification and compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge