Hierarchical robust aggregation of sales forecasts at aggregated levels in e-commerce, based on exponential smoothing and Holt's linear trend method

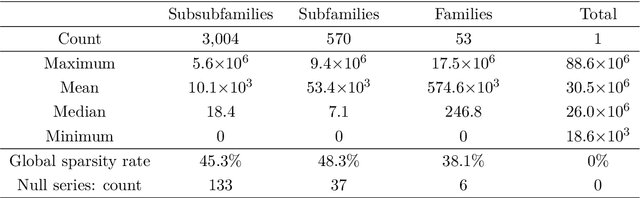
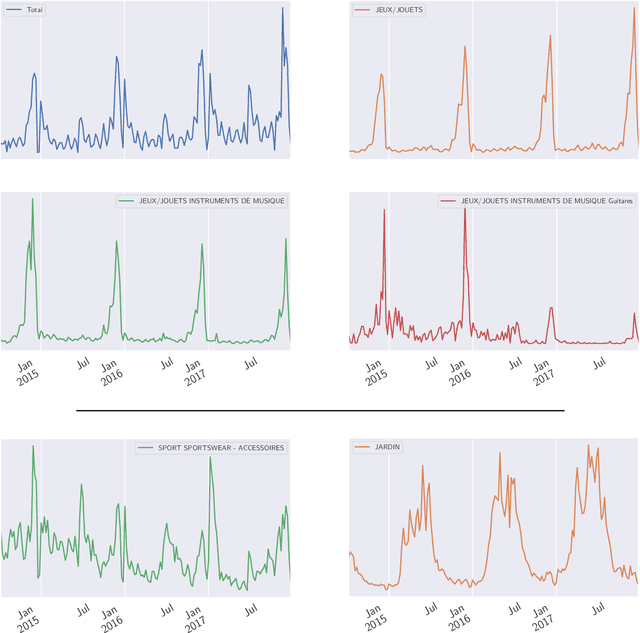
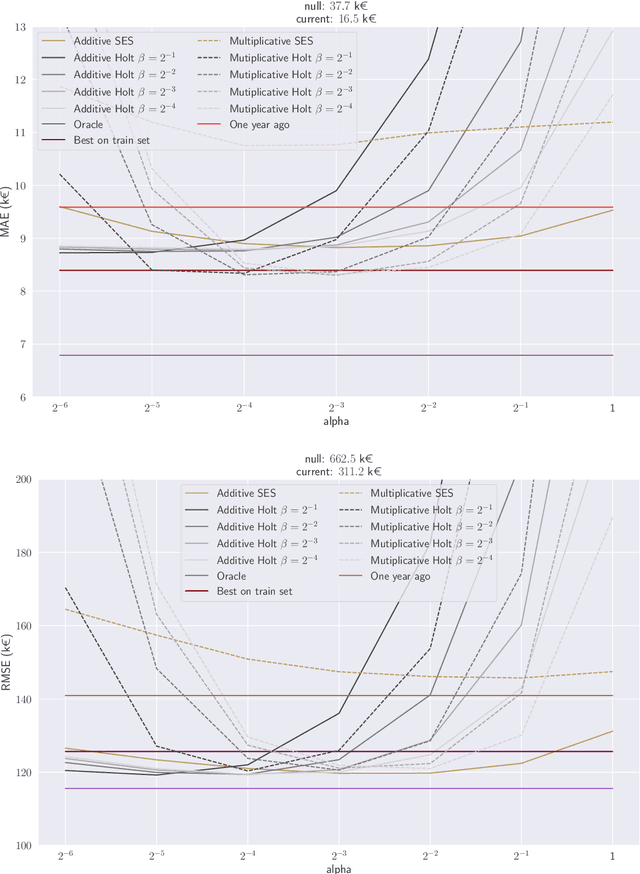
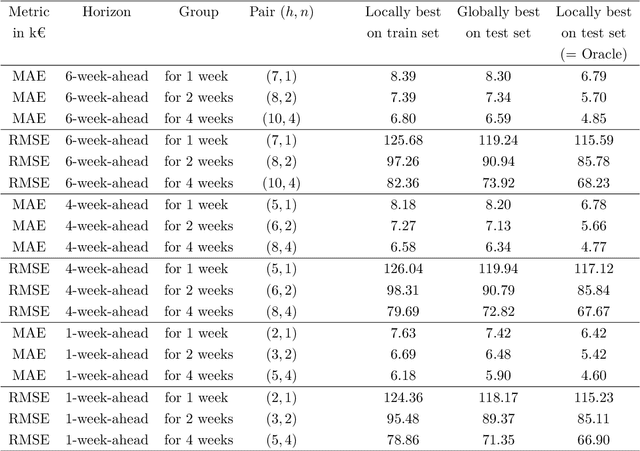
We revisit the interest of classical statistical techniques for sales forecasting like exponential smoothing and extensions thereof (as Holt's linear trend method). We do so by considering ensemble forecasts, given by several instances of these classical techniques tuned with different (sets of) parameters, and by forming convex combinations of the elements of ensemble forecasts over time, in a robust and sequential manner. The machine-learning theory behind this is called "robust online aggregation", or "prediction with expert advice", or "prediction of individual sequences" (see Cesa-Bianchi and Lugosi, 2006). We apply this methodology to a hierarchical data set of sales provided by the e-commerce company Cdiscount and output forecasts at the levels of subsubfamilies, subfamilies and families of items sold, for various forecasting horizons (up to 6-week-ahead). The performance achieved is better than what would be obtained by optimally tuning the classical techniques on a train set and using their forecasts on the test set. The performance is also good from an intrinsic point of view (in terms of mean absolute percentage of error). While getting these better forecasts of sales at the levels of subsubfamilies, subfamilies and families is interesting per se, we also suggest to use them as additional features when forecasting demand at the item level.

Online Hierarchical Forecasting for Power Consumption Data

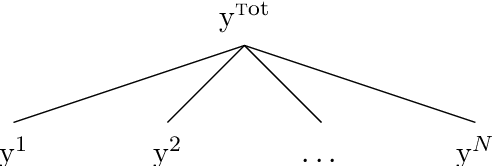
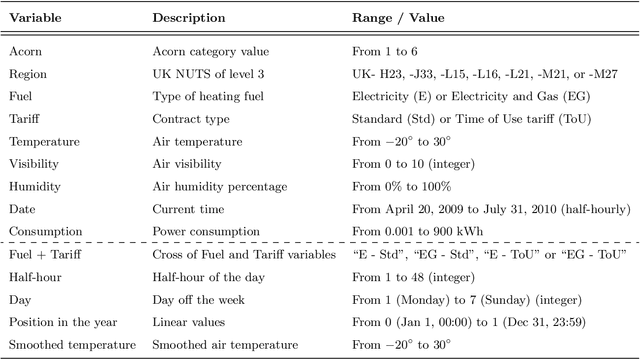
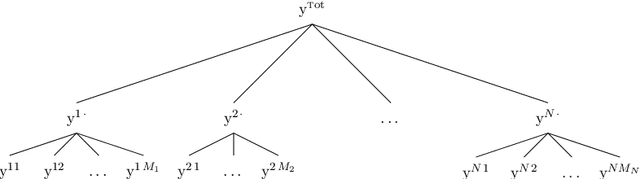
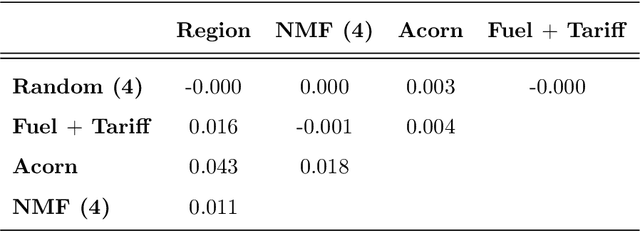
We study the forecasting of the power consumptions of a population of households and of subpopulations thereof. These subpopulations are built according to location, to exogenous information and/or to profiles we determined from historical households consumption time series. Thus, we aim to forecast the electricity consumption time series at several levels of households aggregation. These time series are linked through some summation constraints which induce a hierarchy. Our approach consists in three steps: feature generation, aggregation and projection. Firstly (feature generation step), we build, for each considering group for households, a benchmark forecast (called features), using random forests or generalized additive models. Secondly (aggregation step), aggregation algorithms, run in parallel, aggregate these forecasts and provide new predictions. Finally (projection step), we use the summation constraints induced by the time series underlying hierarchy to re-conciliate the forecasts by projecting them in a well-chosen linear subspace. We provide some theoretical guaranties on the average prediction error of this methodology, through the minimization of a quantity called regret. We also test our approach on households power consumption data collected in Great Britain by multiple energy providers in the Energy Demand Research Project context. We build and compare various population segmentations for the evaluation of our approach performance.

Uniform regret bounds over $R^d$ for the sequential linear regression problem with the square loss

We consider the setting of online linear regression for arbitrary deterministic sequences, with the square loss. We are interested in regret bounds that hold uniformly over all vectors in $u $\in$ R^d$. Vovk (2001) showed a d ln T lower bound on this uniform regret. We exhibit forecasters with closed-form regret bounds that match this d ln T quantity. To the best of our knowledge, earlier works only provided closed-form regret bounds of 2d ln T + O(1).