On the origin of neural scaling laws: from random graphs to natural language

Scaling laws have played a major role in the modern AI revolution, providing practitioners predictive power over how the model performance will improve with increasing data, compute, and number of model parameters. This has spurred an intense interest in the origin of neural scaling laws, with a common suggestion being that they arise from power law structure already present in the data. In this paper we study scaling laws for transformers trained to predict random walks (bigrams) on graphs with tunable complexity. We demonstrate that this simplified setting already gives rise to neural scaling laws even in the absence of power law structure in the data correlations. We further consider dialing down the complexity of natural language systematically, by training on sequences sampled from increasingly simplified generative language models, from 4,2,1-layer transformer language models down to language bigrams, revealing a monotonic evolution of the scaling exponents. Our results also include scaling laws obtained from training on random walks on random graphs drawn from Erdös-Renyi and scale-free Barabási-Albert ensembles. Finally, we revisit conventional scaling laws for language modeling, demonstrating that several essential results can be reproduced using 2 layer transformers with context length of 50, provide a critical analysis of various fits used in prior literature, demonstrate an alternative method for obtaining compute optimal curves as compared with current practice in published literature, and provide preliminary evidence that maximal update parameterization may be more parameter efficient than standard parameterization.

Learning Pseudorandom Numbers with Transformers: Permuted Congruential Generators, Curricula, and Interpretability

We study the ability of Transformer models to learn sequences generated by Permuted Congruential Generators (PCGs), a widely used family of pseudo-random number generators (PRNGs). PCGs introduce substantial additional difficulty over linear congruential generators (LCGs) by applying a series of bit-wise shifts, XORs, rotations and truncations to the hidden state. We show that Transformers can nevertheless successfully perform in-context prediction on unseen sequences from diverse PCG variants, in tasks that are beyond published classical attacks. In our experiments we scale moduli up to $2^{22}$ using up to $50$ million model parameters and datasets with up to $5$ billion tokens. Surprisingly, we find even when the output is truncated to a single bit, it can be reliably predicted by the model. When multiple distinct PRNGs are presented together during training, the model can jointly learn them, identifying structures from different permutations. We demonstrate a scaling law with modulus $m$: the number of in-context sequence elements required for near-perfect prediction grows as $\sqrt{m}$. For larger moduli, optimization enters extended stagnation phases; in our experiments, learning moduli $m \geq 2^{20}$ requires incorporating training data from smaller moduli, demonstrating a critical necessity for curriculum learning. Finally, we analyze embedding layers and uncover a novel clustering phenomenon: the model spontaneously groups the integer inputs into bitwise rotationally-invariant clusters, revealing how representations can transfer from smaller to larger moduli.

When Can You Get Away with Low Memory Adam?

Adam is the go-to optimizer for training modern machine learning models, but it requires additional memory to maintain the moving averages of the gradients and their squares. While various low-memory optimizers have been proposed that sometimes match the performance of Adam, their lack of reliability has left Adam as the default choice. In this work, we apply a simple layer-wise Signal-to-Noise Ratio (SNR) analysis to quantify when second-moment tensors can be effectively replaced by their means across different dimensions. Our SNR analysis reveals how architecture, training hyperparameters, and dataset properties impact compressibility along Adam's trajectory, naturally leading to $\textit{SlimAdam}$, a memory-efficient Adam variant. $\textit{SlimAdam}$ compresses the second moments along dimensions with high SNR when feasible, and leaves when compression would be detrimental. Through experiments across a diverse set of architectures and training scenarios, we show that $\textit{SlimAdam}$ matches Adam's performance and stability while saving up to $98\%$ of total second moments. Code for $\textit{SlimAdam}$ is available at https://github.com/dayal-kalra/low-memory-adam.

Why Warmup the Learning Rate? Underlying Mechanisms and Improvements

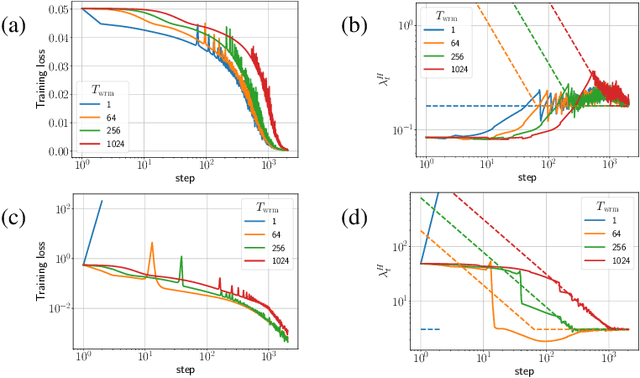
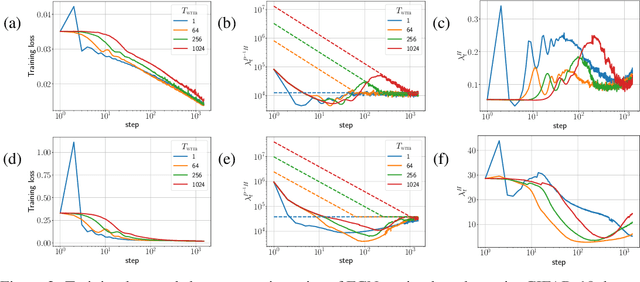
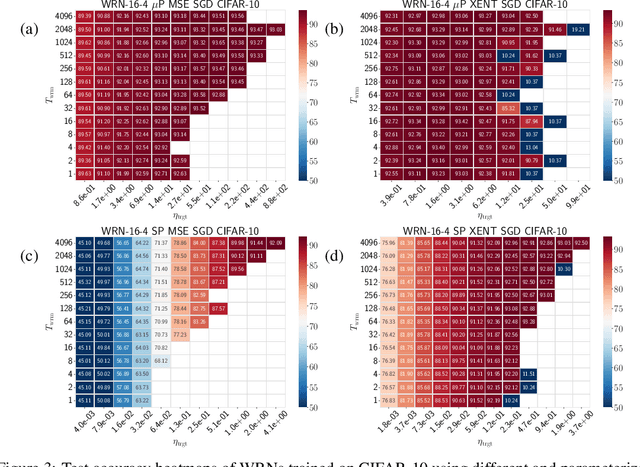
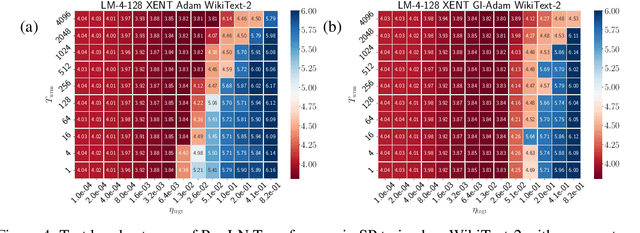
It is common in deep learning to warm up the learning rate $\eta$, often by a linear schedule between $\eta_{\text{init}} = 0$ and a predetermined target $\eta_{\text{trgt}}$. In this paper, we show through systematic experiments using SGD and Adam that the overwhelming benefit of warmup arises from allowing the network to tolerate larger $\eta_{\text{trgt}}$ by forcing the network to more well-conditioned areas of the loss landscape. The ability to handle larger $\eta_{\text{trgt}}$ makes hyperparameter tuning more robust while improving the final performance. We uncover different regimes of operation during the warmup period, depending on whether training starts off in a progressive sharpening or sharpness reduction phase, which in turn depends on the initialization and parameterization. Using these insights, we show how $\eta_{\text{init}}$ can be properly chosen by utilizing the loss catapult mechanism, which saves on the number of warmup steps, in some cases completely eliminating the need for warmup. We also suggest an initialization for the variance in Adam which provides benefits similar to warmup.

Universal Sharpness Dynamics in Neural Network Training: Fixed Point Analysis, Edge of Stability, and Route to Chaos

In gradient descent dynamics of neural networks, the top eigenvalue of the Hessian of the loss (sharpness) displays a variety of robust phenomena throughout training. This includes early time regimes where the sharpness may decrease during early periods of training (sharpness reduction), and later time behavior such as progressive sharpening and edge of stability. We demonstrate that a simple $2$-layer linear network (UV model) trained on a single training example exhibits all of the essential sharpness phenomenology observed in real-world scenarios. By analyzing the structure of dynamical fixed points in function space and the vector field of function updates, we uncover the underlying mechanisms behind these sharpness trends. Our analysis reveals (i) the mechanism behind early sharpness reduction and progressive sharpening, (ii) the required conditions for edge of stability, and (iii) a period-doubling route to chaos on the edge of stability manifold as learning rate is increased. Finally, we demonstrate that various predictions from this simplified model generalize to real-world scenarios and discuss its limitations.

Phase diagram of training dynamics in deep neural networks: effect of learning rate, depth, and width

We systematically analyze optimization dynamics in deep neural networks (DNNs) trained with stochastic gradient descent (SGD) over long time scales and study the effect of learning rate, depth, and width of the neural network. By analyzing the maximum eigenvalue $\lambda^H_t$ of the Hessian of the loss, which is a measure of sharpness of the loss landscape, we find that the dynamics can show four distinct regimes: (i) an early time transient regime, (ii) an intermediate saturation regime, (iii) a progressive sharpening regime, and finally (iv) a late time ``edge of stability" regime. The early and intermediate regimes (i) and (ii) exhibit a rich phase diagram depending on learning rate $\eta \equiv c/\lambda^H_0$, depth $d$, and width $w$. We identify several critical values of $c$ which separate qualitatively distinct phenomena in the early time dynamics of training loss and sharpness, and extract their dependence on $d/w$. Our results have implications for how to scale the learning rate with DNN depth and width in order to remain in the same phase of learning.