A Scalable Measure of Loss Landscape Curvature for Analyzing the Training Dynamics of LLMs

Understanding the curvature evolution of the loss landscape is fundamental to analyzing the training dynamics of neural networks. The most commonly studied measure, Hessian sharpness ($λ_{\max}^H$) -- the largest eigenvalue of the loss Hessian -- determines local training stability and interacts with the learning rate throughout training. Despite its significance in analyzing training dynamics, direct measurement of Hessian sharpness remains prohibitive for Large Language Models (LLMs) due to high computational cost. We analyze $\textit{critical sharpness}$ ($λ_c$), a computationally efficient measure requiring fewer than $10$ forward passes given the update direction $Δ\mathbfθ$. Critically, this measure captures well-documented Hessian sharpness phenomena, including progressive sharpening and Edge of Stability. Using this measure, we provide the first demonstration of these sharpness phenomena at scale, up to $7$B parameters, spanning both pre-training and mid-training of OLMo-2 models. We further introduce $\textit{relative critical sharpness}$ ($λ_c^{1\to 2}$), which quantifies the curvature of one loss landscape while optimizing another, to analyze the transition from pre-training to fine-tuning and guide data mixing strategies. Critical sharpness provides practitioners with a practical tool for diagnosing curvature dynamics and informing data composition choices at scale. More broadly, our work shows that scalable curvature measures can provide actionable insights for large-scale training.

Teaching Pretrained Language Models to Think Deeper with Retrofitted Recurrence

Recent advances in depth-recurrent language models show that recurrence can decouple train-time compute and parameter count from test-time compute. In this work, we study how to convert existing pretrained non-recurrent language models into depth-recurrent models. We find that using a curriculum of recurrences to increase the effective depth of the model over the course of training preserves performance while reducing total computational cost. In our experiments, on mathematics, we observe that converting pretrained models to recurrent ones results in better performance at a given compute budget than simply post-training the original non-recurrent language model.

When Can You Get Away with Low Memory Adam?

Adam is the go-to optimizer for training modern machine learning models, but it requires additional memory to maintain the moving averages of the gradients and their squares. While various low-memory optimizers have been proposed that sometimes match the performance of Adam, their lack of reliability has left Adam as the default choice. In this work, we apply a simple layer-wise Signal-to-Noise Ratio (SNR) analysis to quantify when second-moment tensors can be effectively replaced by their means across different dimensions. Our SNR analysis reveals how architecture, training hyperparameters, and dataset properties impact compressibility along Adam's trajectory, naturally leading to $\textit{SlimAdam}$, a memory-efficient Adam variant. $\textit{SlimAdam}$ compresses the second moments along dimensions with high SNR when feasible, and leaves when compression would be detrimental. Through experiments across a diverse set of architectures and training scenarios, we show that $\textit{SlimAdam}$ matches Adam's performance and stability while saving up to $98\%$ of total second moments. Code for $\textit{SlimAdam}$ is available at https://github.com/dayal-kalra/low-memory-adam.

Why Warmup the Learning Rate? Underlying Mechanisms and Improvements

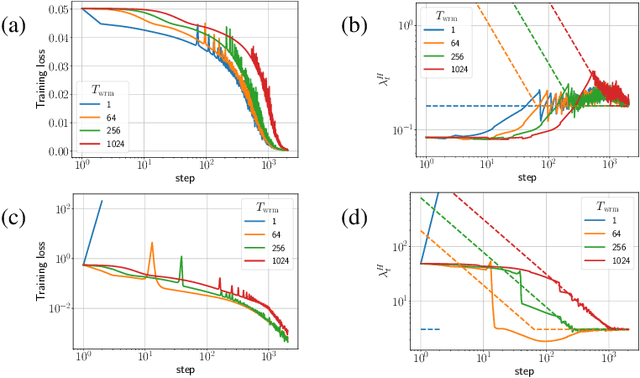
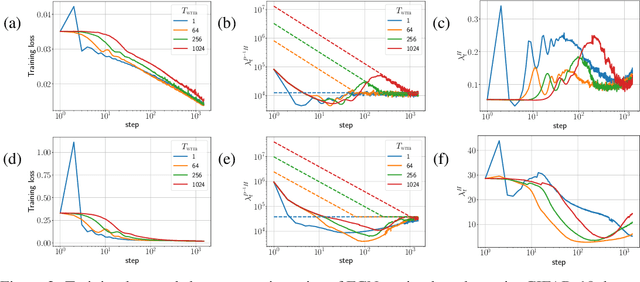
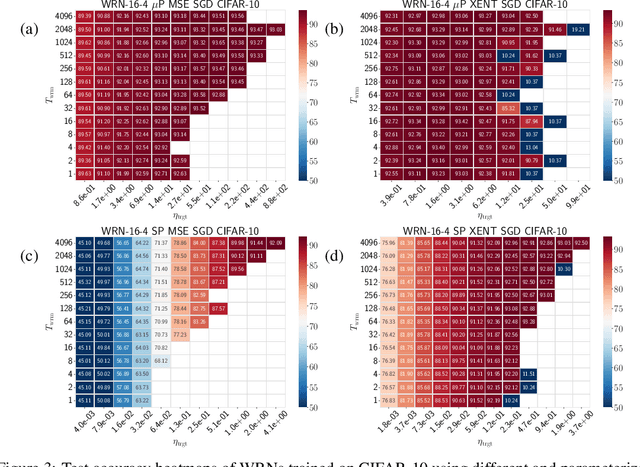
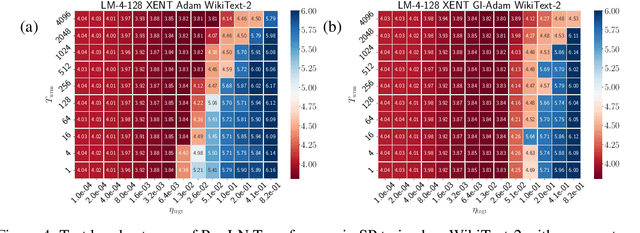
It is common in deep learning to warm up the learning rate $\eta$, often by a linear schedule between $\eta_{\text{init}} = 0$ and a predetermined target $\eta_{\text{trgt}}$. In this paper, we show through systematic experiments using SGD and Adam that the overwhelming benefit of warmup arises from allowing the network to tolerate larger $\eta_{\text{trgt}}$ by forcing the network to more well-conditioned areas of the loss landscape. The ability to handle larger $\eta_{\text{trgt}}$ makes hyperparameter tuning more robust while improving the final performance. We uncover different regimes of operation during the warmup period, depending on whether training starts off in a progressive sharpening or sharpness reduction phase, which in turn depends on the initialization and parameterization. Using these insights, we show how $\eta_{\text{init}}$ can be properly chosen by utilizing the loss catapult mechanism, which saves on the number of warmup steps, in some cases completely eliminating the need for warmup. We also suggest an initialization for the variance in Adam which provides benefits similar to warmup.

Universal Sharpness Dynamics in Neural Network Training: Fixed Point Analysis, Edge of Stability, and Route to Chaos

In gradient descent dynamics of neural networks, the top eigenvalue of the Hessian of the loss (sharpness) displays a variety of robust phenomena throughout training. This includes early time regimes where the sharpness may decrease during early periods of training (sharpness reduction), and later time behavior such as progressive sharpening and edge of stability. We demonstrate that a simple $2$-layer linear network (UV model) trained on a single training example exhibits all of the essential sharpness phenomenology observed in real-world scenarios. By analyzing the structure of dynamical fixed points in function space and the vector field of function updates, we uncover the underlying mechanisms behind these sharpness trends. Our analysis reveals (i) the mechanism behind early sharpness reduction and progressive sharpening, (ii) the required conditions for edge of stability, and (iii) a period-doubling route to chaos on the edge of stability manifold as learning rate is increased. Finally, we demonstrate that various predictions from this simplified model generalize to real-world scenarios and discuss its limitations.

Phase diagram of training dynamics in deep neural networks: effect of learning rate, depth, and width

We systematically analyze optimization dynamics in deep neural networks (DNNs) trained with stochastic gradient descent (SGD) over long time scales and study the effect of learning rate, depth, and width of the neural network. By analyzing the maximum eigenvalue $\lambda^H_t$ of the Hessian of the loss, which is a measure of sharpness of the loss landscape, we find that the dynamics can show four distinct regimes: (i) an early time transient regime, (ii) an intermediate saturation regime, (iii) a progressive sharpening regime, and finally (iv) a late time ``edge of stability" regime. The early and intermediate regimes (i) and (ii) exhibit a rich phase diagram depending on learning rate $\eta \equiv c/\lambda^H_0$, depth $d$, and width $w$. We identify several critical values of $c$ which separate qualitatively distinct phenomena in the early time dynamics of training loss and sharpness, and extract their dependence on $d/w$. Our results have implications for how to scale the learning rate with DNN depth and width in order to remain in the same phase of learning.