Introducing Anisotropic Minkowski Functionals and Quantitative Anisotropy Measures for Local Structure Analysis in Biomedical Imaging

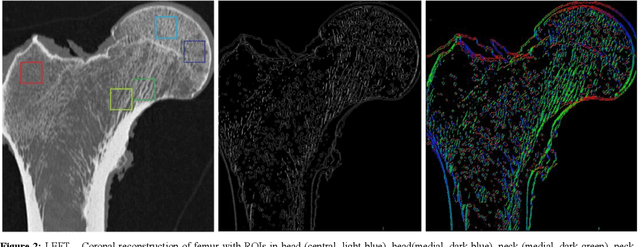
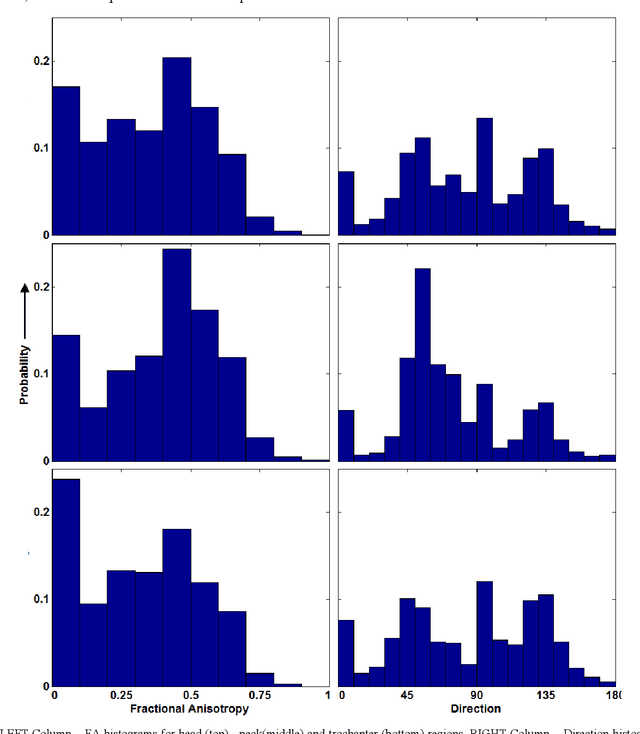
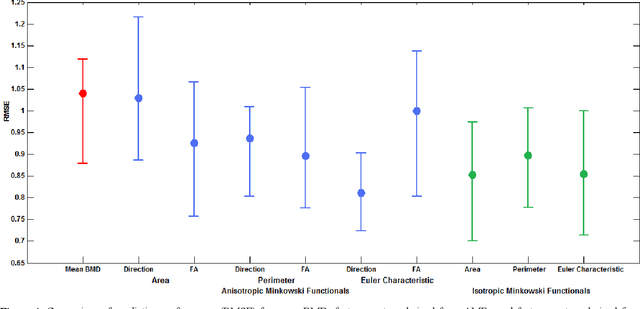
The ability of Minkowski Functionals to characterize local structure in different biological tissue types has been demonstrated in a variety of medical image processing tasks. We introduce anisotropic Minkowski Functionals (AMFs) as a novel variant that captures the inherent anisotropy of the underlying gray-level structures. To quantify the anisotropy characterized by our approach, we further introduce a method to compute a quantitative measure motivated by a technique utilized in MR diffusion tensor imaging, namely fractional anisotropy. We showcase the applicability of our method in the research context of characterizing the local structure properties of trabecular bone micro-architecture in the proximal femur as visualized on multi-detector CT. To this end, AMFs were computed locally for each pixel of ROIs extracted from the head, neck and trochanter regions. Fractional anisotropy was then used to quantify the local anisotropy of the trabecular structures found in these ROIs and to compare its distribution in different anatomical regions. Our results suggest a significantly greater concentration of anisotropic trabecular structures in the head and neck regions when compared to the trochanter region (p < 10-4). We also evaluated the ability of such AMFs to predict bone strength in the femoral head of proximal femur specimens obtained from 50 donors. Our results suggest that such AMFs, when used in conjunction with multi-regression models, can outperform more conventional features such as BMD in predicting failure load. We conclude that such anisotropic Minkowski Functionals can capture valuable information regarding directional attributes of local structure, which may be useful in a wide scope of biomedical imaging applications.

A Framework for Exploring Non-Linear Functional Connectivity and Causality in the Human Brain: Mutual Connectivity Analysis (MCA) of Resting-State Functional MRI with Convergent Cross-Mapping and Non-Metric Clustering

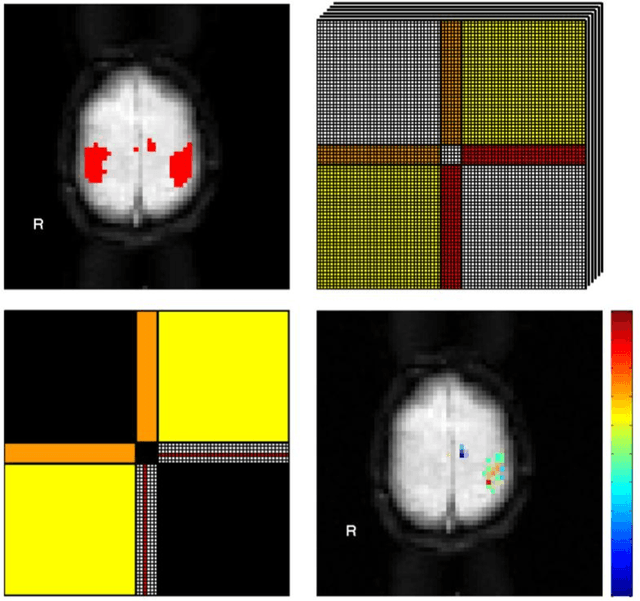
We present a computational framework for analysis and visualization of non-linear functional connectivity in the human brain from resting state functional MRI (fMRI) data for purposes of recovering the underlying network community structure and exploring causality between network components. Our proposed methodology of non-linear mutual connectivity analysis (MCA) involves two computational steps. First, the pair-wise cross-prediction performance between resting state fMRI pixel time series within the brain is evaluated. The underlying network structure is subsequently recovered from the affinity matrix constructed through MCA using non-metric network partitioning/clustering with the so-called Louvain method. We demonstrate our methodology in the task of identifying regions of the motor cortex associated with hand movement on resting state fMRI data acquired from eight slice locations in four subjects. For comparison, we also localized regions of the motor cortex through a task-based fMRI sequence involving a finger-tapping stimulus paradigm. Finally, we integrate convergent cross mapping (CCM) into the first step of MCA for investigating causality between regions of the motor cortex. Results regarding causation between regions of the motor cortex revealed a significant directional variability and were not readily interpretable in a consistent manner across all subjects. However, our results on whole-slice fMRI analysis demonstrate that MCA-based model-free recovery of regions associated with the primary motor cortex and supplementary motor area are in close agreement with localization of similar regions achieved with a task-based fMRI acquisition. Thus, we conclude that our computational framework MCA can extract and visualize valuable information concerning the underlying network structure and causation between different regions of the brain in resting state fMRI.