DeepQMLP: A Scalable Quantum-Classical Hybrid DeepNeural Network Architecture for Classification

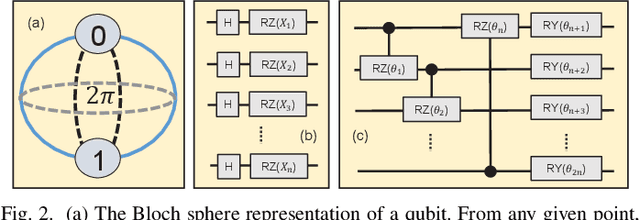
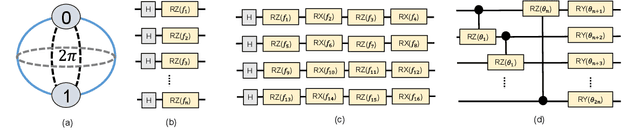
Quantum machine learning (QML) is promising for potential speedups and improvements in conventional machine learning (ML) tasks (e.g., classification/regression). The search for ideal QML models is an active research field. This includes identification of efficient classical-to-quantum data encoding scheme, construction of parametric quantum circuits (PQC) with optimal expressivity and entanglement capability, and efficient output decoding scheme to minimize the required number of measurements, to name a few. However, most of the empirical/numerical studies lack a clear path towards scalability. Any potential benefit observed in a simulated environment may diminish in practical applications due to the limitations of noisy quantum hardware (e.g., under decoherence, gate-errors, and crosstalk). We present a scalable quantum-classical hybrid deep neural network (DeepQMLP) architecture inspired by classical deep neural network architectures. In DeepQMLP, stacked shallow Quantum Neural Network (QNN) models mimic the hidden layers of a classical feed-forward multi-layer perceptron network. Each QNN layer produces a new and potentially rich representation of the input data for the next layer. This new representation can be tuned by the parameters of the circuit. Shallow QNN models experience less decoherence, gate errors, etc. which make them (and the network) more resilient to quantum noise. We present numerical studies on a variety of classification problems to show the trainability of DeepQMLP. We also show that DeepQMLP performs reasonably well on unseen data and exhibits greater resilience to noise over QNN models that use a deep quantum circuit. DeepQMLP provided up to 25.3% lower loss and 7.92% higher accuracy during inference under noise than QMLP.

Quantum-Classical Hybrid Machine Learning for Image Classification (ICCAD Special Session Paper)

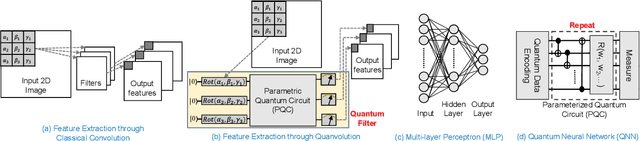
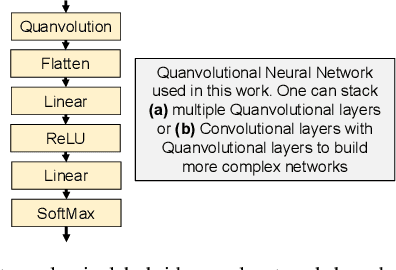
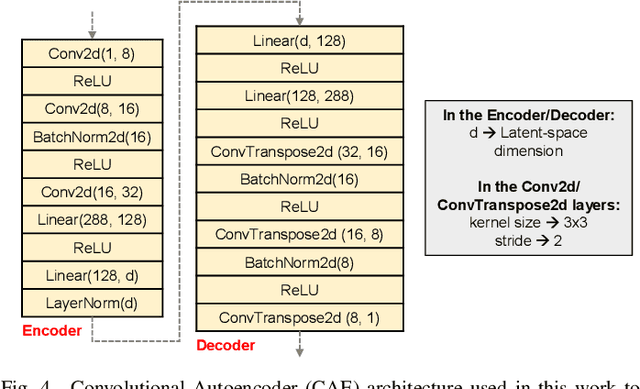
Image classification is a major application domain for conventional deep learning (DL). Quantum machine learning (QML) has the potential to revolutionize image classification. In any typical DL-based image classification, we use convolutional neural network (CNN) to extract features from the image and multi-layer perceptron network (MLP) to create the actual decision boundaries. On one hand, QML models can be useful in both of these tasks. Convolution with parameterized quantum circuits (Quanvolution) can extract rich features from the images. On the other hand, quantum neural network (QNN) models can create complex decision boundaries. Therefore, Quanvolution and QNN can be used to create an end-to-end QML model for image classification. Alternatively, we can extract image features separately using classical dimension reduction techniques such as, Principal Components Analysis (PCA) or Convolutional Autoencoder (CAE) and use the extracted features to train a QNN. We review two proposals on quantum-classical hybrid ML models for image classification namely, Quanvolutional Neural Network and dimension reduction using a classical algorithm followed by QNN. Particularly, we make a case for trainable filters in Quanvolution and CAE-based feature extraction for image datasets (instead of dimension reduction using linear transformations such as, PCA). We discuss various design choices, potential opportunities, and drawbacks of these models. We also release a Python-based framework to create and explore these hybrid models with a variety of design choices.

Drug Discovery Approaches using Quantum Machine Learning

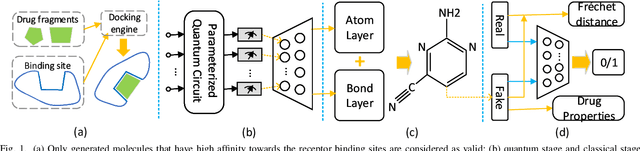
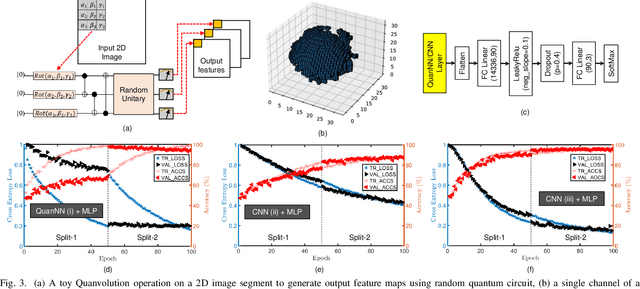
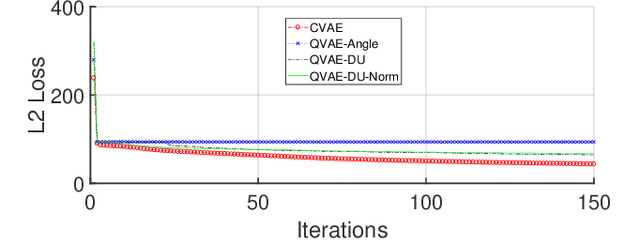
Traditional drug discovery pipeline takes several years and cost billions of dollars. Deep generative and predictive models are widely adopted to assist in drug development. Classical machines cannot efficiently produce atypical patterns of quantum computers which might improve the training quality of learning tasks. We propose a suite of quantum machine learning techniques e.g., generative adversarial network (GAN), convolutional neural network (CNN) and variational auto-encoder (VAE) to generate small drug molecules, classify binding pockets in proteins, and generate large drug molecules, respectively.

Accelerating Quantum Approximate Optimization Algorithm using Machine Learning

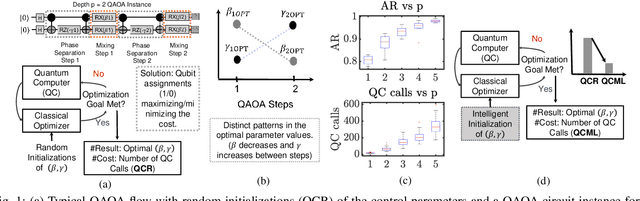
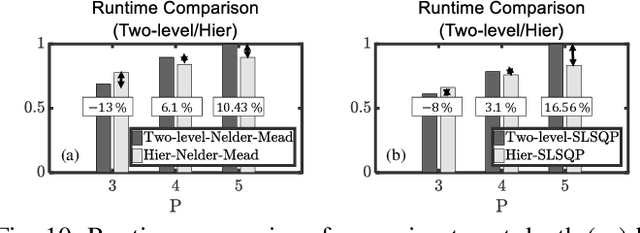
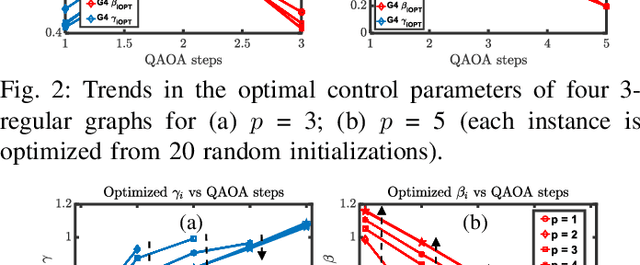
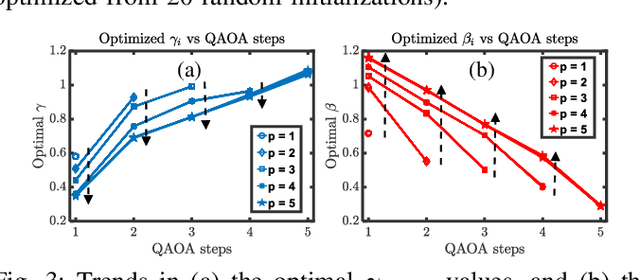
We propose a machine learning based approach to accelerate quantum approximate optimization algorithm (QAOA) implementation which is a promising quantum-classical hybrid algorithm to prove the so-called quantum supremacy. In QAOA, a parametric quantum circuit and a classical optimizer iterates in a closed loop to solve hard combinatorial optimization problems. The performance of QAOA improves with increasing number of stages (depth) in the quantum circuit. However, two new parameters are introduced with each added stage for the classical optimizer increasing the number of optimization loop iterations. We note a correlation among parameters of the lower-depth and the higher-depth QAOA implementations and, exploit it by developing a machine learning model to predict the gate parameters close to the optimal values. As a result, the optimization loop converges in a fewer number of iterations. We choose graph MaxCut problem as a prototype to solve using QAOA. We perform a feature extraction routine using 100 different QAOA instances and develop a training data-set with 13,860 optimal parameters. We present our analysis for 4 flavors of regression models and 4 flavors of classical optimizers. Finally, we show that the proposed approach can curtail the number of optimization iterations by on average 44.9% (up to 65.7%) from an analysis performed with 264 flavors of graphs.