DeepQMLP: A Scalable Quantum-Classical Hybrid DeepNeural Network Architecture for Classification
Paper and Code
Feb 02, 2022
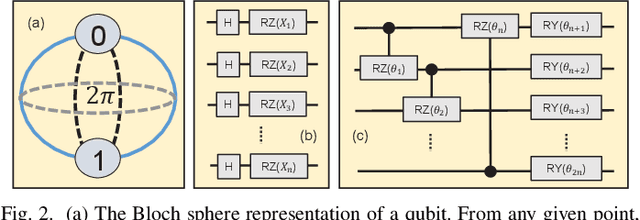


Quantum machine learning (QML) is promising for potential speedups and improvements in conventional machine learning (ML) tasks (e.g., classification/regression). The search for ideal QML models is an active research field. This includes identification of efficient classical-to-quantum data encoding scheme, construction of parametric quantum circuits (PQC) with optimal expressivity and entanglement capability, and efficient output decoding scheme to minimize the required number of measurements, to name a few. However, most of the empirical/numerical studies lack a clear path towards scalability. Any potential benefit observed in a simulated environment may diminish in practical applications due to the limitations of noisy quantum hardware (e.g., under decoherence, gate-errors, and crosstalk). We present a scalable quantum-classical hybrid deep neural network (DeepQMLP) architecture inspired by classical deep neural network architectures. In DeepQMLP, stacked shallow Quantum Neural Network (QNN) models mimic the hidden layers of a classical feed-forward multi-layer perceptron network. Each QNN layer produces a new and potentially rich representation of the input data for the next layer. This new representation can be tuned by the parameters of the circuit. Shallow QNN models experience less decoherence, gate errors, etc. which make them (and the network) more resilient to quantum noise. We present numerical studies on a variety of classification problems to show the trainability of DeepQMLP. We also show that DeepQMLP performs reasonably well on unseen data and exhibits greater resilience to noise over QNN models that use a deep quantum circuit. DeepQMLP provided up to 25.3% lower loss and 7.92% higher accuracy during inference under noise than QMLP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge