Learned transform compression with optimized entropy encoding

We consider the problem of learned transform compression where we learn both, the transform as well as the probability distribution over the discrete codes. We utilize a soft relaxation of the quantization operation to allow for back-propagation of gradients and employ vector (rather than scalar) quantization of the latent codes. Furthermore, we apply similar relaxation in the code probability assignments enabling direct optimization of the code entropy. To the best of our knowledge, this approach is completely novel. We conduct a set of proof-of concept experiments confirming the potency of our approaches.

Improving VAE generations of multimodal data through data-dependent conditional priors

One of the major shortcomings of variational autoencoders is the inability to produce generations from the individual modalities of data originating from mixture distributions. This is primarily due to the use of a simple isotropic Gaussian as the prior for the latent code in the ancestral sampling procedure for the data generations. We propose a novel formulation of variational autoencoders, conditional prior VAE (CP-VAE), which learns to differentiate between the individual mixture components and therefore allows for generations from the distributional data clusters. We assume a two-level generative process with a continuous (Gaussian) latent variable sampled conditionally on a discrete (categorical) latent component. The new variational objective naturally couples the learning of the posterior and prior conditionals, and the learning of the latent categories encoding the multimodality of the original data in an unsupervised manner. The data-dependent conditional priors are then used to sample the continuous latent code when generating new samples from the individual mixture components corresponding to the multimodal structure of the original data. Our experimental results illustrate the generative performance of our new model comparing to multiple baselines.

Large-scale Nonlinear Variable Selection via Kernel Random Features

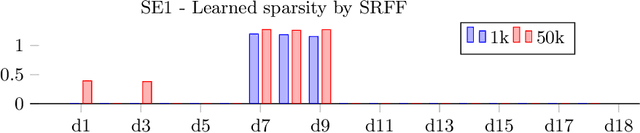
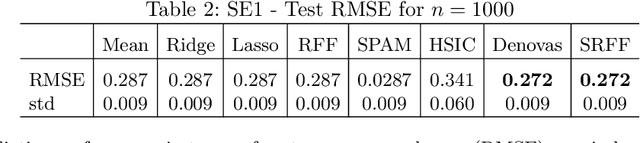
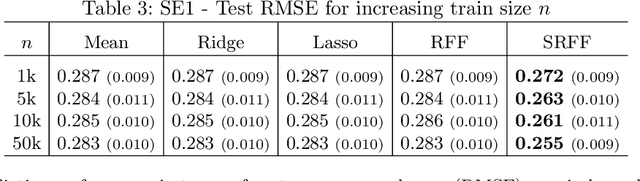
We propose a new method for input variable selection in nonlinear regression. The method is embedded into a kernel regression machine that can model general nonlinear functions, not being a priori limited to additive models. This is the first kernel-based variable selection method applicable to large datasets. It sidesteps the typical poor scaling properties of kernel methods by mapping the inputs into a relatively low-dimensional space of random features. The algorithm discovers the variables relevant for the regression task together with learning the prediction model through learning the appropriate nonlinear random feature maps. We demonstrate the outstanding performance of our method on a set of large-scale synthetic and real datasets.

Structured nonlinear variable selection

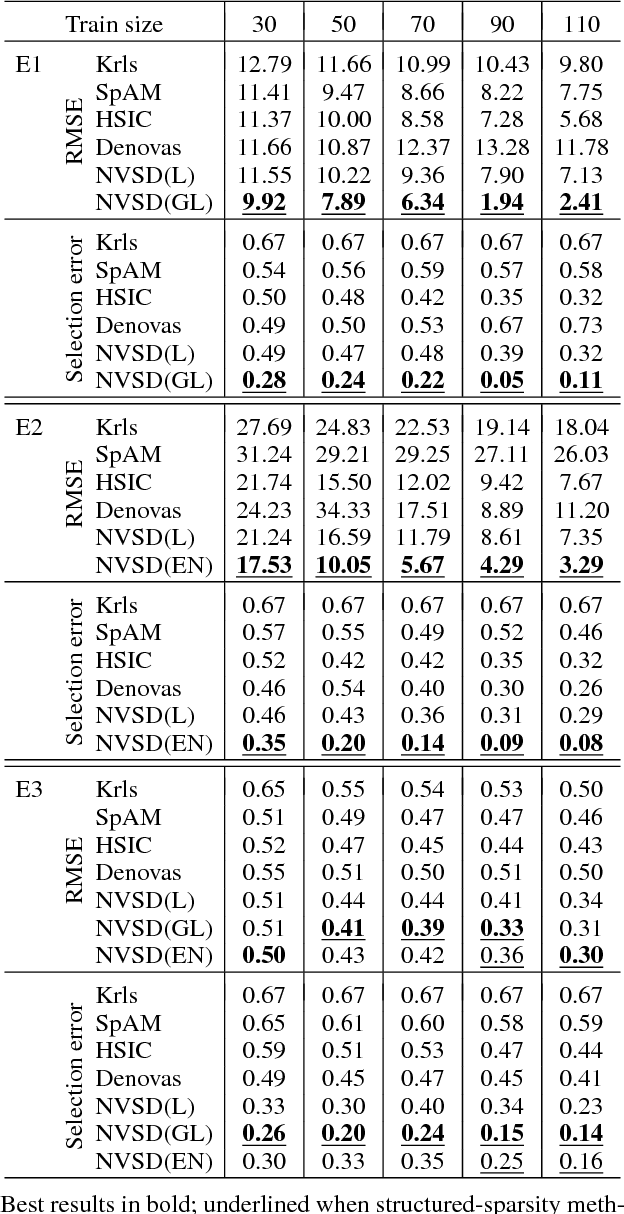
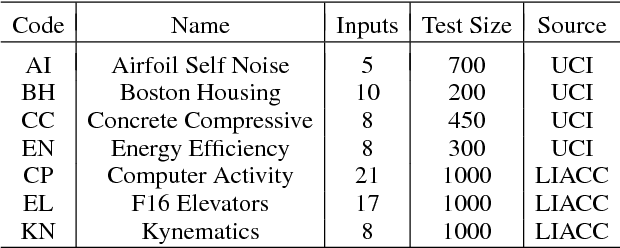
We investigate structured sparsity methods for variable selection in regression problems where the target depends nonlinearly on the inputs. We focus on general nonlinear functions not limiting a priori the function space to additive models. We propose two new regularizers based on partial derivatives as nonlinear equivalents of group lasso and elastic net. We formulate the problem within the framework of learning in reproducing kernel Hilbert spaces and show how the variational problem can be reformulated into a more practical finite dimensional equivalent. We develop a new algorithm derived from the ADMM principles that relies solely on closed forms of the proximal operators. We explore the empirical properties of our new algorithm for Nonlinear Variable Selection based on Derivatives (NVSD) on a set of experiments and confirm favourable properties of our structured-sparsity models and the algorithm in terms of both prediction and variable selection accuracy.

Forecasting and Granger Modelling with Non-linear Dynamical Dependencies

Traditional linear methods for forecasting multivariate time series are not able to satisfactorily model the non-linear dependencies that may exist in non-Gaussian series. We build on the theory of learning vector-valued functions in the reproducing kernel Hilbert space and develop a method for learning prediction functions that accommodate such non-linearities. The method not only learns the predictive function but also the matrix-valued kernel underlying the function search space directly from the data. Our approach is based on learning multiple matrix-valued kernels, each of those composed of a set of input kernels and a set of output kernels learned in the cone of positive semi-definite matrices. In addition to superior predictive performance in the presence of strong non-linearities, our method also recovers the hidden dynamic relationships between the series and thus is a new alternative to existing graphical Granger techniques.