Randomized Rank-Revealing QLP for Low-Rank Matrix Decomposition

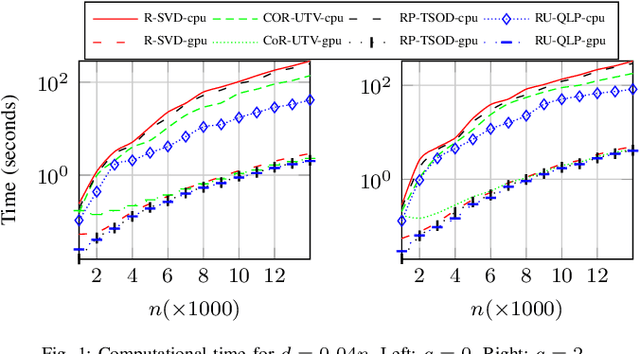
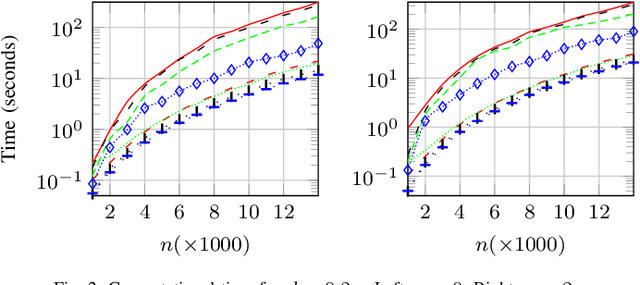
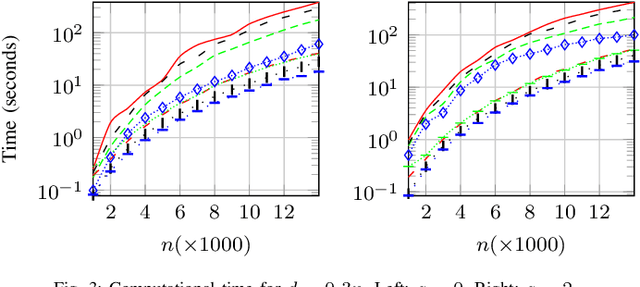
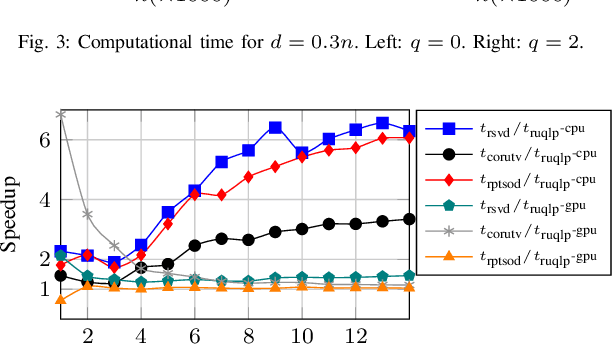
The pivoted QLP decomposition is computed through two consecutive pivoted QR decompositions, and provides an approximation to the singular value decomposition. This work is concerned with a partial QLP decomposition of low-rank matrices computed through randomization, termed Randomized Unpivoted QLP (RU-QLP). Like pivoted QLP, RU-QLP is rank-revealing and yet it utilizes random column sampling and the unpivoted QR decomposition. The latter modifications allow RU-QLP to be highly parallelizable on modern computational platforms. We provide an analysis for RU-QLP, deriving bounds in spectral and Frobenius norms on: i) the rank-revealing property; ii) principal angles between approximate subspaces and exact singular subspaces and vectors; and iii) low-rank approximation errors. Effectiveness of the bounds is illustrated through numerical tests. We further use a modern, multicore machine equipped with a GPU to demonstrate the efficiency of RU-QLP. Our results show that compared to the randomized SVD, RU-QLP achieves a speedup of up to 7.1 times on the CPU and up to 2.3 times with the GPU.

A QLP Decomposition via Randomization

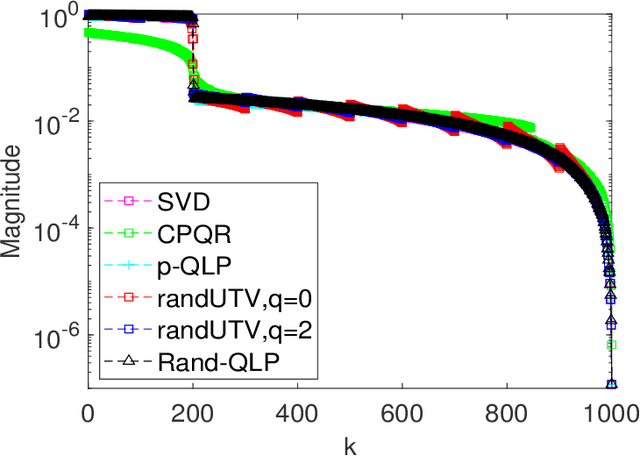
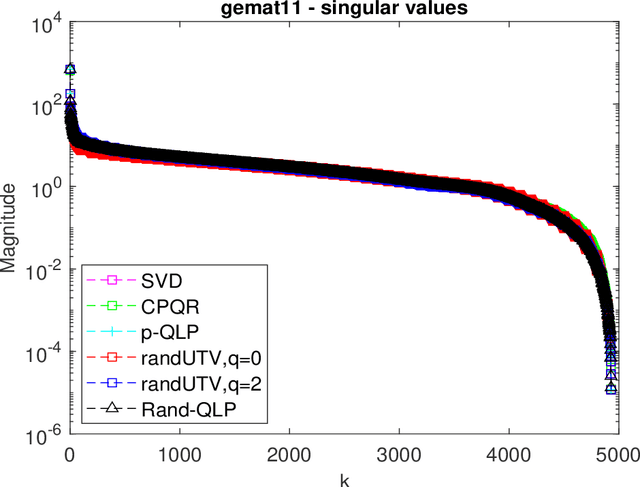
This paper is concerned with full matrix decomposition of matrices, primarily low-rank matrices. It develops a QLP-like decomposition algorithm such that when operating on a matrix A, gives A = QLP^T , where Q and P are orthonormal, and L is lower-triangular. The proposed algorithm, termed Rand-QLP, utilizes randomization and the unpivoted QR decomposition. This in turn enables Rand-QLP to leverage modern computational architectures, thus addressing a serious bottleneck associated with classical and most recent matrix decomposition algorithms. We derive several error bounds for Rand- QLP: bounds for the first k approximate singular values as well as the trailing block of the middle factor, which show that Rand-QLP is rank-revealing; and bounds for the distance between approximate subspaces and the exact ones for all four fundamental subspaces of a given matrix. We assess the speed and approximation quality of Rand-QLP on synthetic and real matrices with different dimensions and characteristics, and compare our results with those of multiple existing algorithms.

Projection-based QLP Algorithm for Efficiently Computing Low-Rank Approximation of Matrices

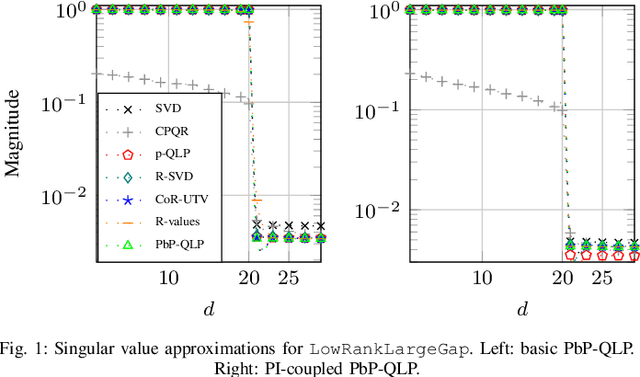
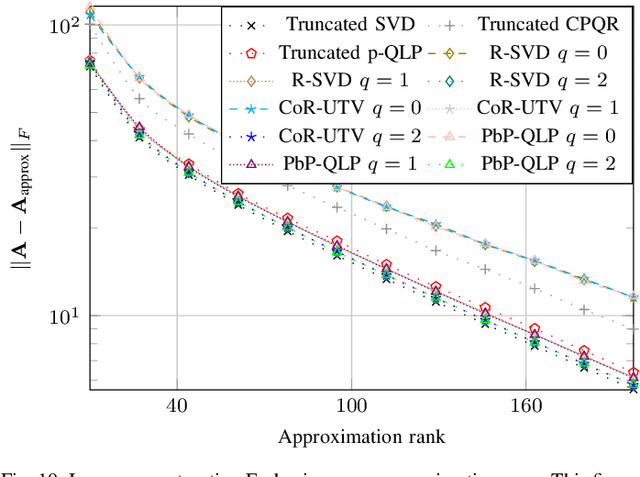
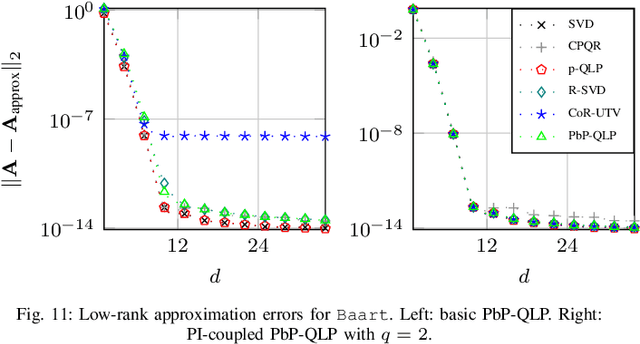
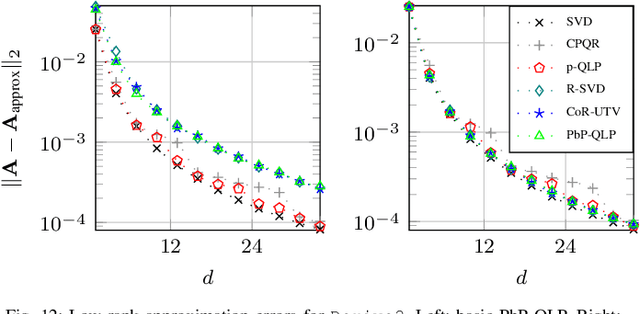
Matrices with low numerical rank are omnipresent in many signal processing and data analysis applications. The pivoted QLP (p-QLP) algorithm constructs a highly accurate approximation to an input low-rank matrix. However, it is computationally prohibitive for large matrices. In this paper, we introduce a new algorithm termed Projection-based Partial QLP (PbP-QLP) that efficiently approximates the p-QLP with high accuracy. Fundamental in our work is the exploitation of randomization and in contrast to the p-QLP, PbP-QLP does not use the pivoting strategy. As such, PbP-QLP can harness modern computer architectures, even better than competing randomized algorithms. The efficiency and effectiveness of our proposed PbP-QLP algorithm are investigated through various classes of synthetic and real-world data matrices.