Predicting breast cancer with AI for individual risk-adjusted MRI screening and early detection

Women with an increased life-time risk of breast cancer undergo supplemental annual screening MRI. We propose to predict the risk of developing breast cancer within one year based on the current MRI, with the objective of reducing screening burden and facilitating early detection. An AI algorithm was developed on 53,858 breasts from 12,694 patients who underwent screening or diagnostic MRI and accrued over 12 years, with 2,331 confirmed cancers. A first U-Net was trained to segment lesions and identify regions of concern. A second convolutional network was trained to detect malignant cancer using features extracted by the U-Net. This network was then fine-tuned to estimate the risk of developing cancer within a year in cases that radiologists considered normal or likely benign. Risk predictions from this AI were evaluated with a retrospective analysis of 9,183 breasts from a high-risk screening cohort, which were not used for training. Statistical analysis focused on the tradeoff between number of omitted exams versus negative predictive value, and number of potential early detections versus positive predictive value. The AI algorithm identified regions of concern that coincided with future tumors in 52% of screen-detected cancers. Upon directed review, a radiologist found that 71.3% of cancers had a visible correlate on the MRI prior to diagnosis, 65% of these correlates were identified by the AI model. Reevaluating these regions in 10% of all cases with higher AI-predicted risk could have resulted in up to 33% early detections by a radiologist. Additionally, screening burden could have been reduced in 16% of lower-risk cases by recommending a later follow-up without compromising current interval cancer rate. With increasing datasets and improving image quality we expect this new AI-aided, adaptive screening to meaningfully reduce screening burden and improve early detection.

Correlated Components Analysis - Extracting Reliable Dimensions in Multivariate Data

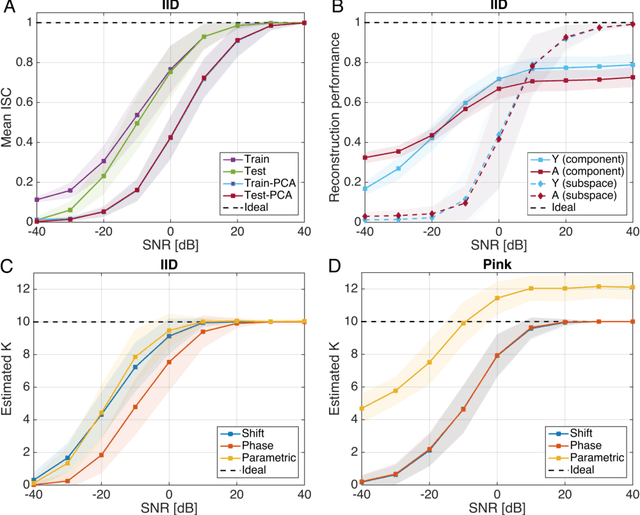
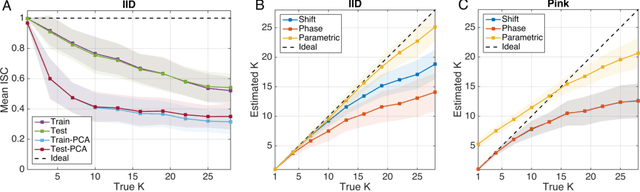
How does one find dimensions in multivariate data that are reliably expressed across repetitions? For example, in a brain imaging study one may want to identify combinations of neural signals that are reliably expressed across multiple trials or subjects. For a behavioral assessment with multiple ratings, one may want to identify an aggregate score that is reliably reproduced across raters. Correlated Components Analysis (CorrCA) addresses this problem by identifying components that are maximally correlated between repetitions (e.g. trials, subjects, raters). Here we formalize this as the maximization of the ratio of between-repetition to within-repetition covariance. We show that this criterion maximizes repeat-reliability, defined as mean over variance across repeats, and that it leads to CorrCA or to multi-set Canonical Correlation Analysis, depending on the constraints. Surprisingly, we also find that CorrCA is equivalent to Linear Discriminant Analysis for equal-mean signals, which provides an unexpected link between classic concepts of multivariate analysis. We provided an exact parametric test for statistical significance based on the F-statistic for normally distributed independent samples, and present and validate shuffle statistics for the case of dependent samples. Regularization and extension to non-linear mappings using kernels are also presented. The algorithms are demonstrated on a series of data analysis applications, and we provide all code and data required to reproduce the results.