Correlated Components Analysis - Extracting Reliable Dimensions in Multivariate Data

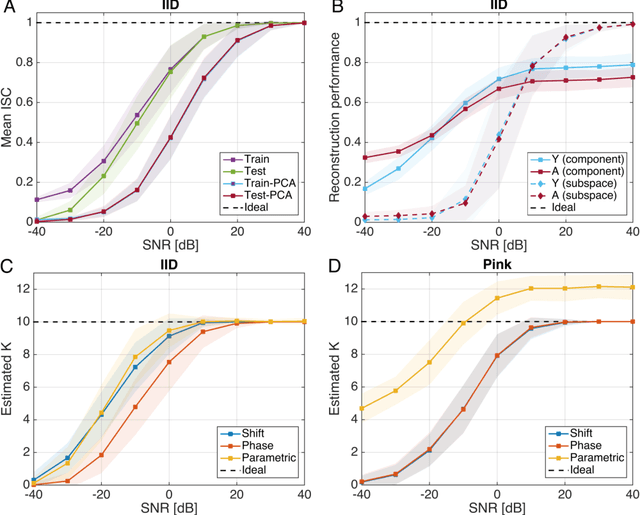
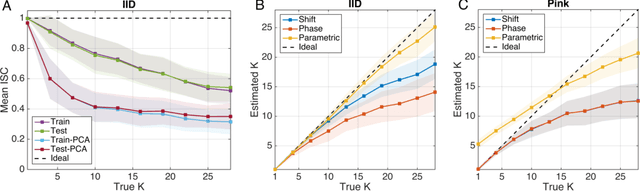
How does one find dimensions in multivariate data that are reliably expressed across repetitions? For example, in a brain imaging study one may want to identify combinations of neural signals that are reliably expressed across multiple trials or subjects. For a behavioral assessment with multiple ratings, one may want to identify an aggregate score that is reliably reproduced across raters. Correlated Components Analysis (CorrCA) addresses this problem by identifying components that are maximally correlated between repetitions (e.g. trials, subjects, raters). Here we formalize this as the maximization of the ratio of between-repetition to within-repetition covariance. We show that this criterion maximizes repeat-reliability, defined as mean over variance across repeats, and that it leads to CorrCA or to multi-set Canonical Correlation Analysis, depending on the constraints. Surprisingly, we also find that CorrCA is equivalent to Linear Discriminant Analysis for equal-mean signals, which provides an unexpected link between classic concepts of multivariate analysis. We provided an exact parametric test for statistical significance based on the F-statistic for normally distributed independent samples, and present and validate shuffle statistics for the case of dependent samples. Regularization and extension to non-linear mappings using kernels are also presented. The algorithms are demonstrated on a series of data analysis applications, and we provide all code and data required to reproduce the results.