Kernel KMeans clustering splits for end-to-end unsupervised decision trees

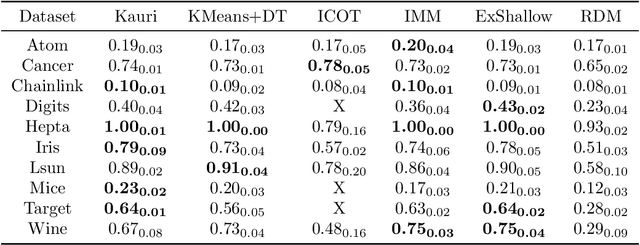
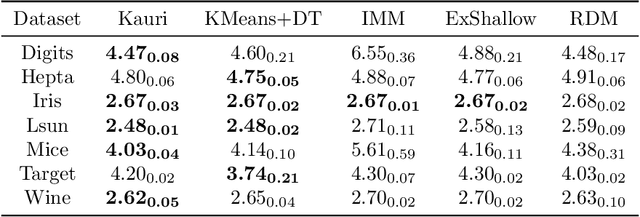
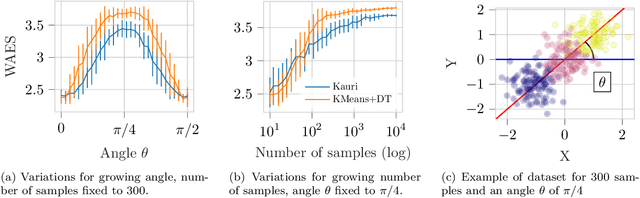
Trees are convenient models for obtaining explainable predictions on relatively small datasets. Although there are many proposals for the end-to-end construction of such trees in supervised learning, learning a tree end-to-end for clustering without labels remains an open challenge. As most works focus on interpreting with trees the result of another clustering algorithm, we present here a novel end-to-end trained unsupervised binary tree for clustering: Kauri. This method performs a greedy maximisation of the kernel KMeans objective without requiring the definition of centroids. We compare this model on multiple datasets with recent unsupervised trees and show that Kauri performs identically when using a linear kernel. For other kernels, Kauri often outperforms the concatenation of kernel KMeans and a CART decision tree.

Generalised Mutual Information: a Framework for Discriminative Clustering

In the last decade, recent successes in deep clustering majorly involved the Mutual Information (MI) as an unsupervised objective for training neural networks with increasing regularisations. While the quality of the regularisations have been largely discussed for improvements, little attention has been dedicated to the relevance of MI as a clustering objective. In this paper, we first highlight how the maximisation of MI does not lead to satisfying clusters. We identified the Kullback-Leibler divergence as the main reason of this behaviour. Hence, we generalise the mutual information by changing its core distance, introducing the Generalised Mutual Information (GEMINI): a set of metrics for unsupervised neural network training. Unlike MI, some GEMINIs do not require regularisations when training as they are geometry-aware thanks to distances or kernels in the data space. Finally, we highlight that GEMINIs can automatically select a relevant number of clusters, a property that has been little studied in deep discriminative clustering context where the number of clusters is a priori unknown.

Sparse GEMINI for Joint Discriminative Clustering and Feature Selection

Feature selection in clustering is a hard task which involves simultaneously the discovery of relevant clusters as well as relevant variables with respect to these clusters. While feature selection algorithms are often model-based through optimised model selection or strong assumptions on $p(\pmb{x})$, we introduce a discriminative clustering model trying to maximise a geometry-aware generalisation of the mutual information called GEMINI with a simple $\ell_1$ penalty: the Sparse GEMINI. This algorithm avoids the burden of combinatorial feature subset exploration and is easily scalable to high-dimensional data and large amounts of samples while only designing a clustering model $p_\theta(y|\pmb{x})$. We demonstrate the performances of Sparse GEMINI on synthetic datasets as well as large-scale datasets. Our results show that Sparse GEMINI is a competitive algorithm and has the ability to select relevant subsets of variables with respect to the clustering without using relevance criteria or prior hypotheses.

Generalised Mutual Information for Discriminative Clustering

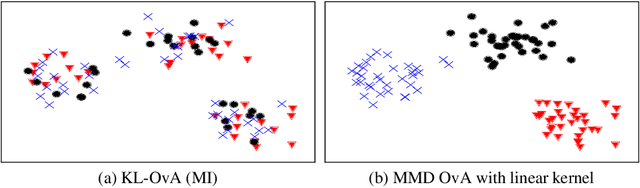
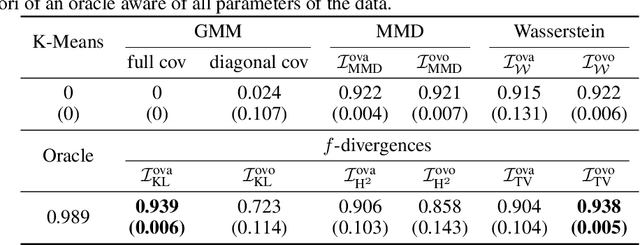
In the last decade, recent successes in deep clustering majorly involved the mutual information (MI) as an unsupervised objective for training neural networks with increasing regularisations. While the quality of the regularisations have been largely discussed for improvements, little attention has been dedicated to the relevance of MI as a clustering objective. In this paper, we first highlight how the maximisation of MI does not lead to satisfying clusters. We identified the Kullback-Leibler divergence as the main reason of this behaviour. Hence, we generalise the mutual information by changing its core distance, introducing the generalised mutual information (GEMINI): a set of metrics for unsupervised neural network training. Unlike MI, some GEMINIs do not require regularisations when training. Some of these metrics are geometry-aware thanks to distances or kernels in the data space. Finally, we highlight that GEMINIs can automatically select a relevant number of clusters, a property that has been little studied in deep clustering context where the number of clusters is a priori unknown.