FiDi-RL: Incorporating Deep Reinforcement Learning with Finite-Difference Policy Search for Efficient Learning of Continuous Control

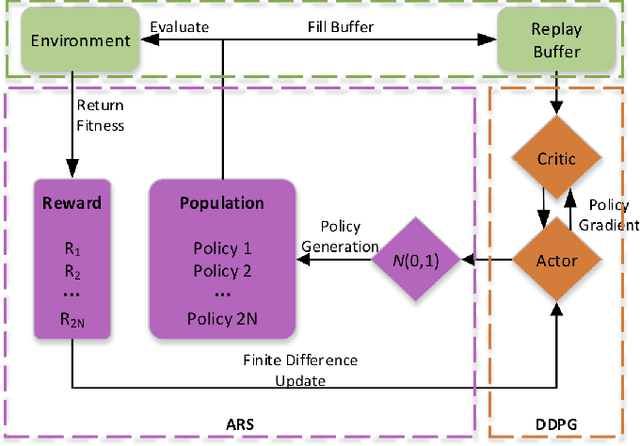
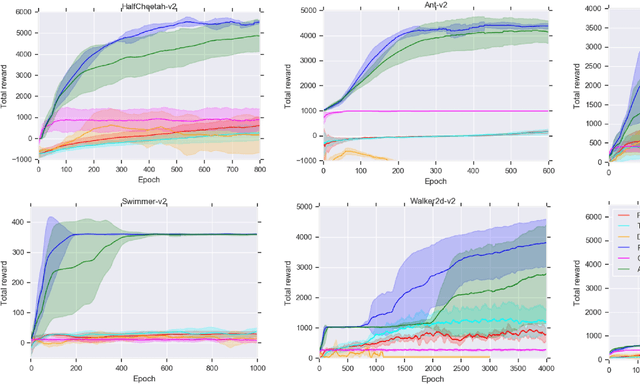
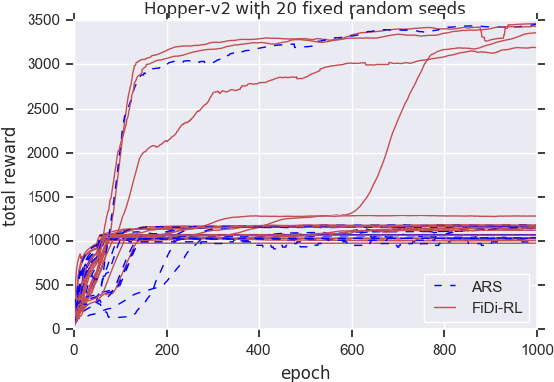
In recent years significant progress has been made in dealing with challenging problems using reinforcement learning.Despite its great success, reinforcement learning still faces challenge in continuous control tasks. Conventional methods always compute the derivatives of the optimal goal with a costly computation resources, and are inefficient, unstable and lack of robust-ness when dealing with such tasks. Alternatively, derivative-based methods treat the optimization process as a blackbox and show robustness and stability in learning continuous control tasks, but not data efficient in learning. The combination of both methods so as to get the best of the both has raised attention. However, most of the existing combination works adopt complex neural networks (NNs) as the policy for control. The double-edged sword of deep NNs can yield better performance, but also makes it difficult for parameter tuning and computation. To this end, in this paper we presents a novel method called FiDi-RL, which incorporates deep RL with Finite-Difference (FiDi) policy search.FiDi-RL combines Deep Deterministic Policy Gradients (DDPG)with Augment Random Search (ARS) and aims at improving the data efficiency of ARS. The empirical results show that FiDi-RL can improves the performance and stability of ARS, and provide competitive results against some existing deep reinforcement learning methods

TBQ($σ$): Improving Efficiency of Trace Utilization for Off-Policy Reinforcement Learning

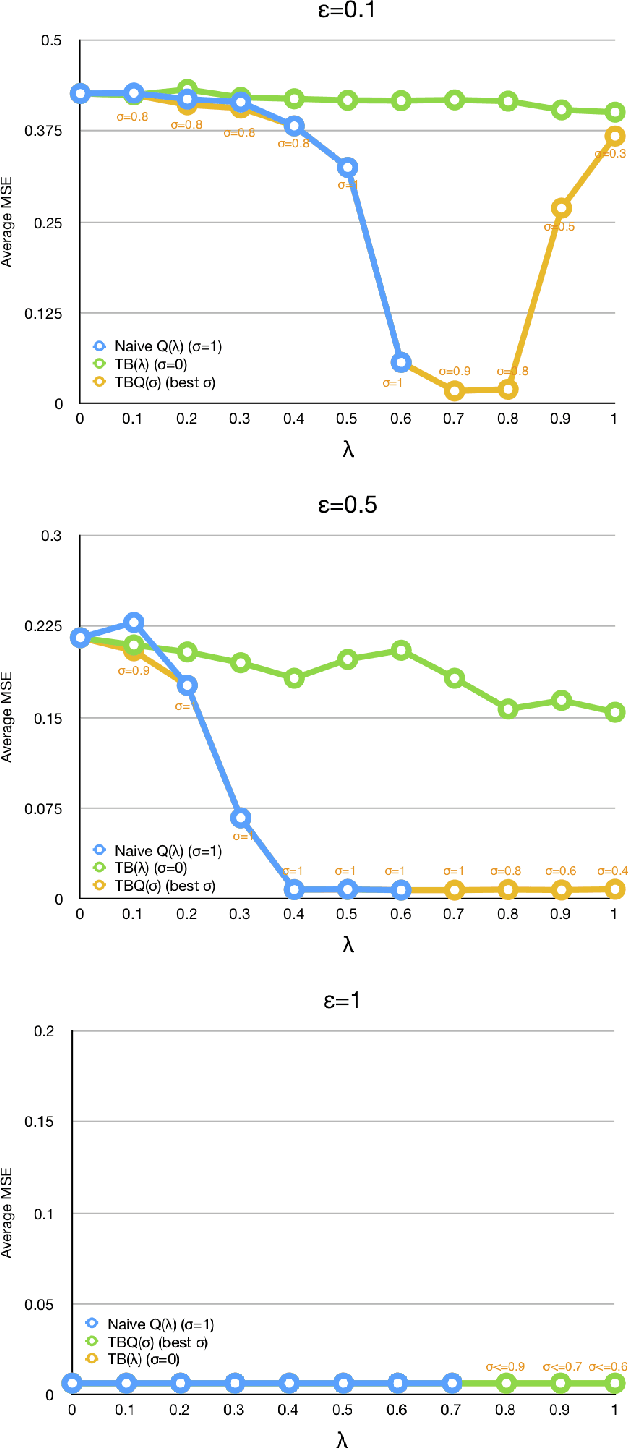
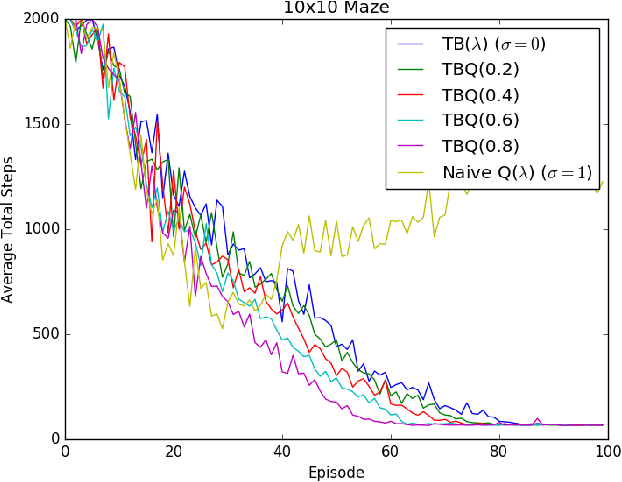
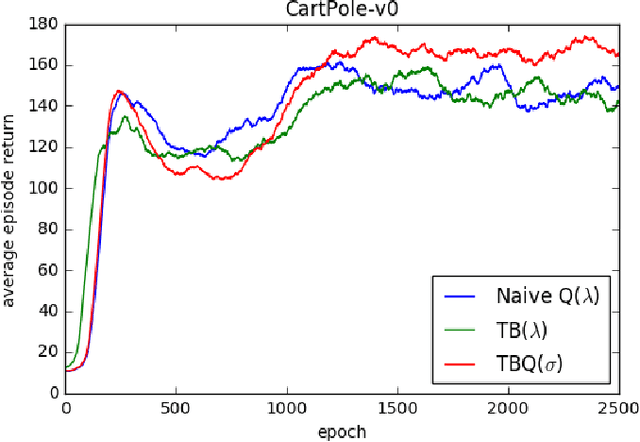
Off-policy reinforcement learning with eligibility traces is challenging because of the discrepancy between target policy and behavior policy. One common approach is to measure the difference between two policies in a probabilistic way, such as importance sampling and tree-backup. However, existing off-policy learning methods based on probabilistic policy measurement are inefficient when utilizing traces under a greedy target policy, which is ineffective for control problems. The traces are cut immediately when a non-greedy action is taken, which may lose the advantage of eligibility traces and slow down the learning process. Alternatively, some non-probabilistic measurement methods such as General Q($\lambda$) and Naive Q($\lambda$) never cut traces, but face convergence problems in practice. To address the above issues, this paper introduces a new method named TBQ($\sigma$), which effectively unifies the tree-backup algorithm and Naive Q($\lambda$). By introducing a new parameter $\sigma$ to illustrate the \emph{degree} of utilizing traces, TBQ($\sigma$) creates an effective integration of TB($\lambda$) and Naive Q($\lambda$) and continuous role shift between them. The contraction property of TB($\sigma$) is theoretically analyzed for both policy evaluation and control settings. We also derive the online version of TBQ($\sigma$) and give the convergence proof. We empirically show that, for $\epsilon\in(0,1]$ in $\epsilon$-greedy policies, there exists some degree of utilizing traces for $\lambda\in[0,1]$, which can improve the efficiency in trace utilization for off-policy reinforcement learning, to both accelerate the learning process and improve the performance.